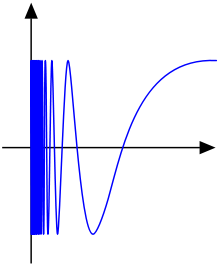
- Seno del topólogo
-
El seno del topólogo, en topología, es una curva contenida en
utilizada frecuentemente para ilustrar determinadas propiedades de los espacios topológicos.[1] Se utiliza especialmente a modo de ejemplo de espacio topológico que es conexo pero no conexo por caminos.Contenido
Definición
Una definición usual del seno del topólogo es la adherencia de la curva
![A=\{(x, \mbox{sen}(\tfrac{1}{x})), \ x \in (0,1]\}](9/0a93184180d2256ceed76893d7a67da7.png)
,
denotada
, y que se define a su vez como la unión de A con su frontera, el segmentoA medida que x se acerca a cero, 1/x crece cada vez más rápido (de hecho, tiende a infinito), por lo que la frecuencia de la curva sinusoidal también es cada vez mayor. En el límite, la frecuencia es infinita.
Variantes
En ocasiones, se considera solamente A, o la unión de A con el punto (0,0). También se puede considerar la función
definida en un intervalo distinto de (0,1],[2] aunque siempre en un intervalo abierto en 0. Incluso se puede hacer distinción entre la «curva cerrada» () y la «curva abierta» (A) del seno del topólogo.[1]Propiedades
La función f(x) = sen(1/x),f(0) = 0 no es de variación acotada.
Como adherencia de una función continua,
es un espacio conexo. Sin embargo, no es conexo por caminos, pues no existe un camino ![f:[0,1] \rightarrow \bar{A}](3/593568e03fe5a0d3d78fbdc60c8e6df2.png)
que una los puntos (1,sen(1)) y (0,0). Para ver que es así, considérese la sucesión formada por los puntos, tomados de derecha a izquierda en la gráfica, cuya segunda componente es alternativamente +1 ó -1. Esta sucesión no converge.Temas relacionados
- Peine del topólogo, otro ejemplo de espacio conexo, pero no conexo por caminos.
Referencias
- ↑ a b Marcelo Salgado. «Relatividad» pág. 29.
- ↑ Gustavo Nevardo Rubiano Ortegón. Fundamentos de topología algebraica. p. 74. http://books.google.com/books?id=Pu_hQnoctzkC.
Categorías:- Curvas
- Topología
![\partial A=\{(0,y), \ y \in [-1,1]\}](7/51733940c0a22b6f6936d3bdc2ae65cb.png)
Wikimedia foundation. 2010.
