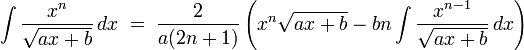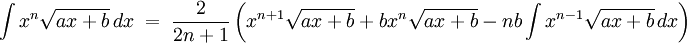Integrales de funciones irracionales
- Integrales de funciones irracionales
-
Anexo:Integrales de funciones irracionales
Wikimedia foundation.
2010.
Mira otros diccionarios:
Lista de integrales de funciones irracionales — La siguiente es una lista de integrales de funciones irracionales … Enciclopedia Universal
Anexo:Integrales de funciones irracionales — La siguiente es una lista de integrales indefinidas de funciones irracionales Contenido 1 Integrales con 2 Integrales con 3 Integrales con 4 Integrales con … Wikipedia Español
Integrales — Anexo:Integrales Saltar a navegación, búsqueda Lista de integrales según el tipo de función: Lista de integrales de funciones racionales Lista de integrales de funciones irracionales Lista de integrales de funciones trigonométricas Lista de… … Wikipedia Español
Anexo:Integrales — Lista de integrales según el tipo de función: Lista de integrales de funciones racionales Lista de integrales de funciones irracionales Lista de integrales de funciones trigonométricas Lista de integrales de funciones hiperbólicas Lista de… … Wikipedia Español
Lista de integrales — según el tipo de función: ● Lista de integrales de funciones racionales ● Lista de integrales de funciones irracionales ● Lista de integrales de funciones trigonométricas ● Lista de integrales de funciones hiperbólicas ● Lista de integrales de… … Enciclopedia Universal
Fórmulas de reducción para integrales — Anexo:Fórmulas de reducción para integrales Saltar a navegación, búsqueda En ocasiones la integración definida o indefinida de funciones de una variable se facilita mediante las llamadas fórmulas de reducción. Son éstas una cierta forma de poner… … Wikipedia Español
Anexo:Fórmulas de reducción para integrales — En ocasiones la integración definida o indefinida de funciones de una variable se facilita mediante las llamadas fórmulas de reducción. Son éstas una cierta forma de poner en relación integrales que, además de depender de una determinada variable … Wikipedia Español
Historia de la matemática — Página del Compendio de cálculo por el método de completado y balanceado de Muhammad ibn Mūsā al Khwārizmī (820 d.C.) La historia de las matemáticas es el área de estudio que abarca las investigaciones sobre los orígenes de los descubrimi … Wikipedia Español
Anexo:Matemáticos importantes — En esta lista de matemáticos importantes se presenta una selección de matemáticos desde la antigüedad hasta el presente. La selección se orienta por los aportes científicos, utilizando como criterio para definir el grado de notoriedad la atención … Wikipedia Español
Número π — π (pi) es la relación entre la longitud de una circunferencia y su diámetro, en geometría euclidiana. Es un número irracional y una de las constantes matemáticas más importantes. Se emplea frecuentemente en matemáticas, física e ingeniería. El… … Wikipedia Español
 ...
...
 Categorías: Integrales | Anexos:Matemáticas
Categorías: Integrales | Anexos:Matemáticas
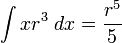
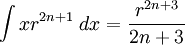
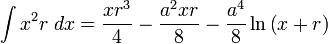
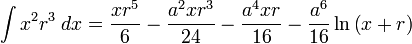
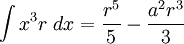
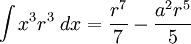
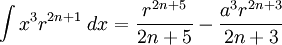
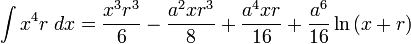
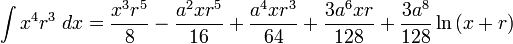
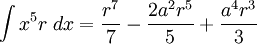
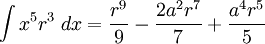
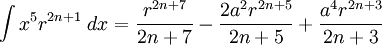
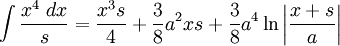
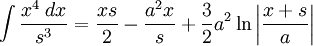
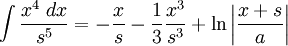
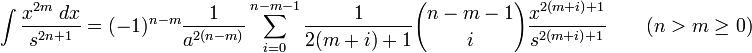
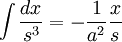
![\int\frac{dx}{s^5}=\frac{1}{a^4}\left[\frac{x}{s}-\frac{1}{3}\frac{x^3}{s^3}\right]](/pictures/eswiki/57/976ffe1b77aeafaba971eee9d6a05163.png)
![\int\frac{dx}{s^7}
=-\frac{1}{a^6}\left[\frac{x}{s}-\frac{2}{3}\frac{x^3}{s^3}+\frac{1}{5}\frac{x^5}{s^5}\right]](/pictures/eswiki/100/d8c21f20257e0ca63e5c22e228f30ac7.png)
![\int\frac{dx}{s^9}
=\frac{1}{a^8}\left[\frac{x}{s}-\frac{3}{3}\frac{x^3}{s^3}+\frac{3}{5}\frac{x^5}{s^5}-\frac{1}{7}\frac{x^7}{s^7}\right]](/pictures/eswiki/102/fcaa9b35840c23cf8e54ef1a46bf39b9.png)
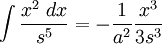
![\int\frac{x^2\;dx}{s^7}
= \frac{1}{a^4}\left[\frac{1}{3}\frac{x^3}{s^3}-\frac{1}{5}\frac{x^5}{s^5}\right]](/pictures/eswiki/49/10d9eca1dd15754f7b6c8cd4a66aa8bf.png)
![\int\frac{x^2\;dx}{s^9}
= -\frac{1}{a^6}\left[\frac{1}{3}\frac{x^3}{s^3}-\frac{2}{5}\frac{x^5}{s^5}+\frac{1}{7}\frac{x^7}{s^7}\right]](/pictures/eswiki/53/54c28b6ef015b425f44119203c27e5be.png)