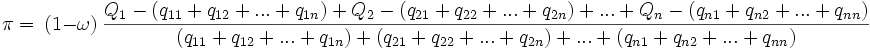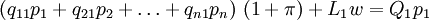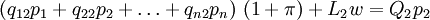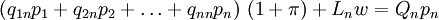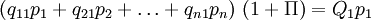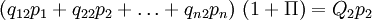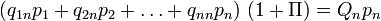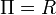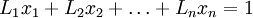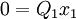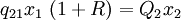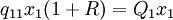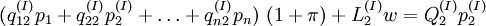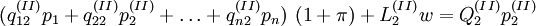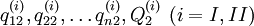- Producción de mercancías por medio de mercancías
-
Producción de mercancías por medio de mercancías
Producción de mercancías por medio de mercancías. Preludio a una crítica de la teoría económica (Produzione di merci a mezzo di merci. Premesse a una critica della teoría económica) es un libro publicado en 1960 y constituye la obra principal de Piero Sraffa (1898 - 1983).
Propósitos e hipótesis del análisis de Piero Sraffa
Primero que todo es conveniente señalar los objetivos y las hipótesis de partida, para que no haya equívocos acerca del alcance real del modelo sraffiano.
Los objetivos
Diversos autores han planteado que la teoría de Sraffa fue originada por la exigencia de resolver aquellos problemas que surgen en la teoría ricardiana cuando se abandona la hipótesis de que sólo existe capital circulante y que la composición del capital es uniforme en todos los sectores.
El problema que Sraffa resolvió en Producción de Mercancías por Medio de Mercancías es indudablemente aquel que preocupó a David Ricardo en todas sus obras: independizar el estudio de la distribución de la renta de la teoría del valor. Sraffa logró encontrar la mercancía numerario que tanto buscó Ricardo, resolviendo además el problema de hacer posible la determinación de la tasa de beneficios (en el caso de que la tasa de salarios sea dada exógenamente) antes de determinar los precios y en forma independiente.
Además, en Producción también hay una crítica implícita a toda la construcción marginalista. El subtítulo de la obra es Preludio a una crítica de la teoría económica y en el Prefacio Sraffa afirma:
Es, sin embargo, un rasgo particular de la serie de proposiciones que ahora se publican que, aunque no se adentran en el examen de la teoría marginalista del valor y de la distribución, fueron concebidas, no obstante, para que sirvieran de base a una crítica de dicha teoría. Si la base se sostiene, la crítica se podrá intentar más tarde, bien sea por el autor o por alguien más joven y mejor equipado para la tarea.
Y “la base” se ha sostenido porque se ha reconocido que las críticas son válidas, aún por parte de los principales teóricos del marginalismo (como Paul Samuelson), que en un comienzo intentaron rechazarlas. El análisis del desplazamiento de los métodos de producción, que Sraffa desarrolla en la tercera parte de Producción, tuvo efectos destructivos sobre las nociones tradicionales. Las ideas básicas de la teoría neoclásica de la producción, que durante medio siglo fueron el fundamento de la economía política –el capital como uno de los factores de producción, la tasa de beneficios como precio y, por tanto, racionador óptimo del factor capital, la función de producción en términos de capital y trabajo, las isocuantas, la productividad marginal del capital, el efecto de sustitución entre factores productivos cuando varían las variables distributivas– demostraron ser fundamentos defectuosos.
También se ha dicho que Sraffa quizá desarrolló su análisis gracias a la contribución de John Von Neumann, quien publicó en 1945 un escrito –cuyo título, en la traducción inglesa a cargo de Nicholas Kaldor es A model of general economic equilibrium– en el que trataba el problema del desplazamiento de los métodos de producción en términos análogos. Sraffa seguramente conoció la obra, y fue citado por David Gawen Champernowne, quien estuvo a cargo del apéndice matemático de la traducción inglesa, por la ayuda que le prestó.
Las hipótesis
Los rendimientos a escala
Sraffa se inclinaba a acoger la hipótesis de rendimientos constantes a escala, en contraste con la literatura marginalista que suponía rendimientos decrecientes a escala.
Es claro que esa hipótesis no es necesaria para la validez del modelo; en efecto, según el mismo Sraffa:
No se considera variación alguna en el volumen de producción ni (al menos en las Partes I y II) variación alguna en las proporciones en las que se usan los diversos medios de producción en cada industria, de modo que ni siquiera surge la pregunta acerca de si los rendimientos son constantes o variables.
Lo que interesa a Sraffa es analizar, rebus sic stantibus, las relaciones entre las variaciones de las variables distributivas y de los precios:
Este punto de vista, que es el de los economistas clásicos, ha sido sumergido y olvidado desde el advenimiento de la teoría “neoclásica”, centrada necesariamente en la variación, porque sin variación no puede haber producto marginal ni costo marginal.
Es necesario –advierte además el autor– estar atentos para no confundir los márgenes espúreos con los márgenes auténticos. En estas páginas se encontrarán ejemplos que, a primera vista, no parecen distintos de los ejemplos de producción marginal; pero el signo seguro de que son espúreos es la ausencia de toda variación del tipo requerido (1960, Prefacio pp. V-VI).
El estado reintegrativo con excedente
Dejando de lado el caso de “producción de subsistencia” que expone en el primer capítulo, Sraffa examina un sistema económico en una situación reintegrativa con excedente, en otras palabras, un sistema en el que la cantidad producida de cada bien es suficiente para reintegrar los medios de producción (estado reintegrativo stricto sensu) y, para al menos un bien, mayor que la cantidad utilizada de ese mismo bien como medio de producción.
Algunos autores han considerado que ese estado es equivalente al estado estacionario, en el que las cantidades producidas de los bienes individuales no varían con el paso del tiempo. En realidad, Sraffa no se pregunta por el uso del excedente al final del periodo de producción; es indiferente que se consuma o se acumule, y en este segundo caso sólo cambiarían las cantidades absolutas producidas en el periodo subsiguiente.
Salario de subsistencia y salario excedente
En el modelo sraffiano, el salario se paga al final del periodo de producción; el fondo de salarios no es contabilizado, entonces, dentro del capital anticipado. El abandono de la concepción de un salario anticipado por la capitalista, propia de los economistas clásicos, es estrictamente una consecuencia de la fallida distinción de los dos elementos del salario: de subsistencia y excedente. El primero está dado en términos reales e indica el conjunto de bienes estrictamente necesarios para la subsistencia de los trabajadores y que, como tales, figuran entre los medios de producción (este fue el único componente que consideraron los economistas clásicos). El segundo, que sólo es determinado post factum, es decir, la producción realizada, mide en cambio la parte del excedente realizado que se asigna a los trabajadores.
Aunque se inclinó a considerar por separado los dos componentes, en sintonía con su formación clásica, en homenaje a la tradición neoclásica Sraffa decidió no hacer tal distinción. El autor mismo advierte, sin embargo, que el inconveniente de esta elección es la diversidad de funciones que cumplen los bienes destinados al consumo de subsistencia dentro del sistema; mejor, y anticipando conceptos que ilustraremos más adelante, la consecuencia es que estos bienes “quedan ipso facto relegados al limbo de los productos no básicos”.
La variable distributiva exógena
La teoría de Sraffa logra determinar la estructura de precios y una de las dos variables distributivas (la tasa de beneficios o de salarios), dada la otra variable y la tecnología. Por tanto, falta decidir cuál de las dos variables se debe considerar independiente y de qué modo determinarla.
Sraffa se inclina a la fijación exógena de la tasa de beneficios, porque, cuando se abandona la hipótesis clásica del salario anclado en niveles de subsistencia y se supone que el salario está dado en términos de una unidad de medida más o menos abstracta, no se puede determinar hasta que se deterrminen los precios de las mercancías.
En el caso de que la tasa de beneficios sea la variable exógena, las soluciones pueden ser:
- suponer como hipótesis que es determinada en el mercado monetario;
- ligarla a la tasa de crecimiento para estudiar el modelo en un contexto dinámico;
- suponer que es fijada en una economía de planificación centralizada mediante el logro de determinatos objetivos;
- referirse a una tasa media de beneficios que los empresarios consideran normal en conexión con la situación particular de la economía en un período dado.
El modelo de producción simple
La primera parte de Producción
Siguiendo la clasificación que Léon Walras utilizó en Elements d’économie politique pure, un clásico de la teoría marginalista en el que se analiza el equilibrio económico general, Producción se divide en tres partes: en la primera se trata el caso más sencillo de producción simple, en el que cada industria produce un solo bien y sólo existe capital circulante; en la segunda se introduce la hipótesis de producción conjunta y se incluyen el capital fijo y los recursos escasos; y en la tercera se trata el problema de la elección de la técnica.
Los métodos de producción (el conjunto de ecuaciones que relacionan los medios de producción con los productos) se suponen dados en las dos primeras partes, mientras que se consideran como incógnitas en la tercera.
La producción de subsistencia
Sraffa, en sintonía con Ricardo, da una representación del sistema económico focalizada en torno a las relaciones entre industrias.
Se tienen las mercancías 1, 2,... n, cada una producida por una industria diferente. Sean
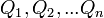 las cantidades producidas anualmente de las mercancías 1, 2,... n, respectivamente. Sean, además,
las cantidades producidas anualmente de las mercancías 1, 2,... n, respectivamente. Sean, además, 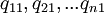 las cantidades de las mercancías 1, 2,... n que usa anualmente la industria que produce el bien 1;
las cantidades de las mercancías 1, 2,... n que usa anualmente la industria que produce el bien 1; 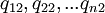 las cantidades correspondientes que usa la industria que produce la mercancía 2, y así sucesivamentre. Las condiciones de producción asumen la forma siguiente:
las cantidades correspondientes que usa la industria que produce la mercancía 2, y así sucesivamentre. Las condiciones de producción asumen la forma siguiente:Cabe señalar que no es necessario suponer que todas las mercancías entran directamente en la producción de las demás; por tanto, algunas de las cantidades de los primeros términos de las ecuaciones pueden ser iguales a cero.
Dada la hipótesis de estado reintegrativo del sistema, la suma de la primera columna ((
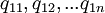 ) será igual a la primera línea (
) será igual a la primera línea (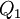 ), la suma de la segunda columna igual a la segunda línea, etc. Para que esta condición ulterior se satisfaga, esto implica que cada una de las n ecuaciones del sistema depende de las demás.
), la suma de la segunda columna igual a la segunda línea, etc. Para que esta condición ulterior se satisfaga, esto implica que cada una de las n ecuaciones del sistema depende de las demás.Dadas estas condiciones, existirá una serie única de valores de cambio (
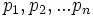 ) que, al ser adoptados por el mercado, permitirán restablecer la distribución original de los productos, creando así las condiciones necesarias para que el proceso se pueda renovar.
) que, al ser adoptados por el mercado, permitirán restablecer la distribución original de los productos, creando así las condiciones necesarias para que el proceso se pueda renovar.Cabe señalar que, en vista de las hipótesis, esos valores surgen directamente de los métodos de producción.
La producción con excedente
Cuando se pasa de la hipótesis de un estado reintegrativo stricto sensu a la de un estado reintegrativo con excedente surgen dificultades, debido a que en el sistema económico el excedente generado se distribuye en proporción a los medios de producción anticipados (el capital), pero una proporción semejante, integrada por los medios de producción de mercancías heterogéneas, no se puede determinar independientemente de los precios.
Podemos definir a la relación entre el producto neto del sistema y la suma de las mercancías utilizadas como medios de producción como tasa de excedente y representarla como R, pero dicha relación no tendría sentido con respecto a las cantidades, porque las mercancías no son homogéneas.
Únicamente la referencia a los precios de las mercancías individuales podría dar sentido a la relación. Por tanto, parecería que no es posible determinar esta tasa independientemente de los precios.
El sistema patrón
Determinación de la tasa de excedente en foma independiente de los precios
Consideremos, sin embargo, un sistema (Sraffa lo denomina sistema patrón) en el que las diversas mercancías se producen en la misma proporción en la que se encuentran en el conjunto de medios de producción; en tal caso
De modo que:
En estas relaciones las cantidades que se comparan corresponden a mercancías homogéneas. Ahora bien, puesto que:podemos escribir:
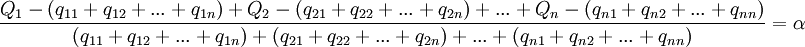 (1)
(1)
El numerador de esta relación no es más que el producto neto generado por el sistema, mientras que el denominador representa los medios de producción anticipados. La ecuación anterior determina entonces la tasa de excedente:
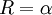 (2)
(2)
Además, R indica la proporción en que la cantidad producida de cada mercancía excede a la cantidad que se utiliza como medio de producción o bien la relación entre el excedente total de las mercancías con respecto a las cantidades utilizadas en la producción, donde dicha relación tiene sentido, es decir, en el sistema patrón.
La posibilidad de hablar de una proporción entre dos grupos de mercancías heterogéneas, sin necesidad de reducirlas a una medida común de precio se debe entonces a la circunstancia de que ambos grupos están formados por las mismas proporciones.
Siendo esta una relación entre cantidades,
el resultado no se modificaría si multiplicáramos las mercancías individuales por los precios. [...] Y dicha relación tampoco se modificaría si, después de multiplicar las mercancías por sus precios, estos precios empezaran a variar por su propia cuenta en direcciones y magnitudes diferentes (Sraffa, 1960, pag. 27).
La mercancía patrón
Sraffa denomina producto neto patrón al excedente total de las mercancías en el sistema patrón, es decir, al producto neto del sistema patrón.
Dada la manera de construir el sistema patrón, el producto neto patrón está formado por las mismas mercancías, combinadas en las mismas proporciones, que se encuentran en el conjunto de los medios de producción del sistema.
El producto neto patrón se puede concebir también como una mercancía compuesta particular en las que las mercancías del sistema entran en proporciones bien determinadas. Sraffa denomina mercancía patrón a esta mercancía compuesta o a cualquier múltiplo o submúltiplo de ella.
Determinación de la tasa de beneficios en forma independiente de los precios
Lo que se ha dicho sobre la relación entre producto neto y medios de producción se puede repetir tal cuál si en lugar del producto neto no referimos a un submúltiplo de él: dicha relación es determinada independientemente de la estructura de los precios y se mantiene invariable cualquiera que sea la variación de estos últimos.
Supongamos entonces que el salario es una fracción del producto neto patrón. Sea ω la porción de dicho producto que va a los salarios. La parte del producto neto que irá a los beneficios será la restante, es decir:
La tasa de beneficios se puede expresar entonces de la siguiente manera:De las ecuaciones 1 y 2 se deriva:
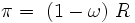 (3)
(3)
La tasa de beneficios del sistema patrón se presenta así como una relación entre cantidades de mercancías, sin necesidad de recurrir a sus precios.La relación entre la tasa de beneficios y la tasa de salarios es lineal: la primera aumenta en proporción directa a una reducción de la segunda.
El sistema de precios
Pasemos ahora a examinar el sistema desde el punto de vista de los precios. Indicando con
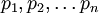 los precios de las mercancías 1, 2,... n, con
los precios de las mercancías 1, 2,... n, con 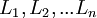 las cantidades de trabajo que se emplean anualmente en las industrias que producen las mercancías 1, 2,... n respectivamente, con una tasa de salarios w y recordando lo que se dijo acerca de la hipótesis de Sraffa de un salario que se paga post factum, podemos representar el sistema económico como sigue:
las cantidades de trabajo que se emplean anualmente en las industrias que producen las mercancías 1, 2,... n respectivamente, con una tasa de salarios w y recordando lo que se dijo acerca de la hipótesis de Sraffa de un salario que se paga post factum, podemos representar el sistema económico como sigue:En caso de que todo el producto excedente del sistema vaya al capital, el sistema asumirá la forma siguiente:
Donde Π indica la tasa de beneficios máxima: la tasa de beneficios que se obtiene en el caso de que todo el producto neto generado por el sistema vaya a los beneficios.
Tasa de excedente y tasa de beneficios máxima
Retomemos ahora lo que se dijo de la tasa de excedente en el sistema patrón: esta no sólo representa la relación entre el producto neto y los medios de producción, sino, puesto que el resultado no se modifica al hacer referencia a los precios, también la relación entre el valor del producto neto y el valor de los medios de producción.
Esta segunda relación no es otra cosa que la tasa de beneficios máxima; por consiguiente:
Ahora, sustituyendo en la ecuación (3), tenemos que:
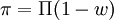 (4)
(4)
La mercancía patrón como numerario
Sobre la validez de la relación entre tasa de beneficios y salario en el sistema efectivo
La ecuación (4) aún nos puede interesar sólo si es posible demostrar que su validez no se limita al sistema patrón imaginario sino que se puede extender al sistema económico real. Se trata, en otras palabras de ver, dice Sraffa, “si la importancia que la mercancía patrón tiene en esta relación se basa en el hecho de que es la sustancia de la que están formados la renta nacional y los medios de producción o en el hecho de que representa la medida en la que se expresan los salarios”. En la primera hipótesis la relación sólo será válida para el sistema patrón; en la segunda, en cambio, también seguirá siendo válida en el sistema efectivo, a condición de que los salarios se expresen en términos de la mercancía patrón apropriada.[1]
Repasando los pasajes que se han desarrollado hasta ahora se podría llegar a la conclusión de que la primera hipótesis es verdadera, pues la determinación de la tasa de beneficios en términos físicos parece ser posible debido a la particular construcción del sistema patrón: en efecto, en dicho sistema, la relación entre la cantidad producida de qualquier mercancía y la cantidad utilizada como medio de producción es la misma para todas las mercancías.
Pero el sistema efectivo está formado por las mismas ecuaciones básicas que forman el sistema patrón, sólo que en proporciones diferentes; de modo que, una vez esté dado el salario, la tasa de beneficios se determina en ambos sistemas independientemente de las proporciones en que aparecen en las ecuaciones de uno u otro sistema. [...] La relación lineal entre el salario y la tasa de beneficios es entonces válida en cualquier caso, con la única condición de que el salario se exprese en términos del producto patrón. La misma tasa de beneficios que se obtiene en el sistema patrón como una relación entre cantidades de mercancías, resultará en el sistema efectivo de una relación entre valores agregados (1960, pp. 29-30).
Consideremos por ejemplo un sistema patrón en el que la tasa de excedente sea del 20% y 3/4 de la renta nacional patrón vayan a los salarios; la tasa de beneficios será del 5%. En el sistema efectivo correspondiente, si los salarios se siguen expresando en términos de la mercancía patrón, la tasa de beneficios seguirá siendo del 5%. Cabe observar, sin embargo, que en este último caso “la participación de los beneficios consistirá en lo que quede de la renta nacional efectiva, y no de la renta patrón, después de deducir el equivalente a 3/4 del producto neto patrón: y los precios deberán ser tales que el valor de lo que va a los beneficios sea igual al 5% del valor de los medios de producción efectivos de la sociedad”.[2]
Constitución de la mercancía patrón
Dijimos que el sistema patrón está formado por las mismas ecuaciones básicas de las que consta el sistema efectivo, sólo que en proporciones diferentes. De esto se sigue que, dado un sistema efectivo, la búsqueda del sistema patrón correspondiente se reduce a la búsqueda de multiplicadores apropriados que, aplicados a las industrias respectivas del sistema original, determinan una expansión (si son mayores que 1) o una contracción (si son menores que 1). Dichos multiplicadores(
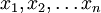 )deberán ser tales que las cantidades resultantes de las distintas mercancías tengan entre sí las mismas proporciones en el lado derecho de las ecuaciones (es decir, como como productos) que las que tienen en el conjunto del lado izquierdo (es decir, como medios de producción). Esto implica que la tasa de excedente (R) es igual para todas las industrias.
)deberán ser tales que las cantidades resultantes de las distintas mercancías tengan entre sí las mismas proporciones en el lado derecho de las ecuaciones (es decir, como como productos) que las que tienen en el conjunto del lado izquierdo (es decir, como medios de producción). Esto implica que la tasa de excedente (R) es igual para todas las industrias.La condición mencionada se puede expresar mediante un sistema de ecuaciones que contiene las mismas constantes (las cuales representan las cantidades de mercancías) que se encuentran en las ecuaciones de la producción del sistema efectivo considerado, pero dispuestas de manera diferente, es decir, de tal manera que las columnas de uno correspondan a las filas del otro. Este sistema es el siguiente:
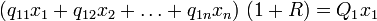
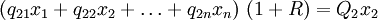 (5)
(5)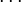
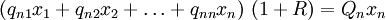
Hay n ecuaciones con n + 1 incógnitas (los n multiplicadores mas R).Para resolver el sistema se podría hacer uno de los multiplicadores igual a 1; sin embargo, de este modo sólo se determinaría la estructura de producción (las proporciones de producción de los diferentes procesos) y no la escala de producción (la producción agregada). Dado que esta última es determinada por la cantidad de fuerza trabajo empleada, y puesto que queremos que dicha cantidad sea igual a la del sistema efectivo, definamos la unidad mediante una ecuación complementaria que contiene esta condición, es decir:
donde L1, L2,... L3 son las cantidades de trabajo que se emplean anualmente en las industrias que producen las mercancías 1, 2,... n respectivamente y, con base en esta ecuación ulterior de normalización, expresan fracciones del trabajo anual de la sociedad, tomado como unidad.
Ahora es posible determinar todas las incógnitas.
Existencia y unicidad del sistema patrón
En este punto es necesario demostrar que para todo sistema efectivo existe el sistema patrón correspondiente, es decir, que existe una serie de n multiplicadores (x), donde n es el número de industrias del sistema considerado, no negativos y no todos nulos, y una tasa de excedente (R) tales que la proporción en que cada mercancía producida se encuentra en el conjunto de los medios de producción en la misma proporción para cada mercancía.
Es necesario demostrar, además, no sólo que existe dicho sistema patrón, sino también que es único, para que, dado un sistema efectivo, la tasa de excedente y la mercancía patrón en la que se miden los salarios sean únicas.
En Producción, Sraffa logra probar la existencia y la unicidad del sistema patrón, presentando demostraciones que se pueden considerar como aplicaciones particulares de teoremas de Perron-Frobenius para las matrices no negativas.
Productos básicos y productos no básicos
La hipótesis de un sistema en estado reintegrativo con excedente implica la posibilidad de que existan “bienes de lujo”, es decir, mercancías que no se utilizan en la producción de las demás mercancías, ni como instrumentos de producción ni como medios de subsistencia. Por el contrario, cuando se considera el caso de producción de subsistencia, todas las mercancías deben encontrarse tanto entre los productos como entre los medios de producción.
Observando el modo en que hemos construido el sistema patrón, partiendo del sistema efectivo, vemos que los multiplicadores asociados a las industrias que producen los bienes de lujo son nulos; estas mercancías no forman parte, entonces, de la mercancía patrón. Un cambio en los procesos productivos que afecte exclusivamente a uno de dichos bienes sólo tendría consecuencias sobre su precio, y no influiría mínimamente en los precios relativos de los demás ni en la tasa de beneficios. Sraffa los denomina bienes no básicos (o mercancías no básicas).
En cambio, denomina bienes básicos (o mercancías básicas) a los que que entran, de modo directo o indirecto, en la producción de todas las mercancías. Las condiciones de producción de dichas mercancías influyen en la determinación de la estructura de precios o de la tasa de beneficios. Si la cantidad producida de una sola de estas mercancías fuese cero, la producción de todas las mercancías, básicas y no básicas, debería ser necesariamente cero.
Una característica del sistema económico que estamos considerando, y que hasta ahora se ha supuesto implícitamente, es la existencia de al menos un producto básico. Si no fuese así, no nos encontraríamos frente a un “sistema económico” verdadero y apropiado, sino frente a sistemas yuxtapuestos.
Hay que señalar finalmente que lo que se ha dicho de las mercancías no básicas también es válido para los productos que se utilizan en la producción de otros productos no básicos, entre los cuales se pueden incluir ellos mismos. En efecto, si una mercancía de esta especie sólo se utilizara en la producción de una mercancía no básica de la especie considerada antes, es claro que correría la suerte de aquella y su multiplicador sería también nulo.
Por ejemplo, si la mercancía 2 sólo entrara en la producción de la mercancía no básica 1 las dos primeras ecuaciones de (5) serían:
Ahora bien,
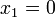 , seguirá
, seguirá 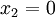 .
.Si luego se utiliza en su propia producción, la relación entre su cantidad como producto y su cantidad como medio de producción será independiente de R, y por esta razón es en general incompatibile con el sistema patrón.
En efecto, si la mercancía 1 sólo fuese utilizada como medio de producción propio la ecuación correspondiente a (5) se convertiría en:
En esta ecuación, cualquiera que fuese el valor que asuma el multiplicador, no incidiría en la tasa de excedente; por consiguiente o bien la tasa de excedente del proceso es exactamente la del sistema patrón que se busca –y entonces x1 podría asumir cualquier valor[3]– o bien la tasa de excedente que se busca no es la que se encuentra en el proceso, y entonces el único valor de x1 que podría satisfacer la ecuación es 0.
Resumiendo, podemos distinguir tres tipos de productos no básicos:
1. productos que no se encuentran entre los medios de producción de ninguna industria; 2. productos que sólo se encuentran entre sus propios medios de producción; 3. productos que sólo se encuentran entre los medios de producción de un grupo de productos no básicos relacionados entre sí.
La parte III de Producción
El desplazamiento de los métodos de producción en el modelo de producción simple
Hasta ahora se ha supuesto que para cada mercancía sólo se dispone de un método de producción, de modo que las variaciones en la distribución de la renta no pueden influir de ninguna manera en los procesos de producción utilizados. La última parte de Producción se dedica precisamente a tratar el caso en que, por el contrario, para una o más mercancías existen uno o más métodos de producción.
Para poder elegir entre posibilidades alternativas es necesario adoptar un criterio de elección. Sraffa supone que ese criterio es el de la rentabilidad y más precisamente que, sea cuales fueren las características institucionales, cuando nos encontremos frente a más de un proceso técnico alternativo para producir la misma mercancía, elijamos aquel que tenga el costo mínimo.
En el tratamineto que sigue definiremos la tecnología como el conjunto de todos los procesos productivos disponibles y la técnica como cualquier subconjunto de estos procesos tal que haya un proceso y sólo uno para cada mercancía producida.
Las elecciones técnicas (choice of technique) para las mercancías no básicas
Supongamos inicialmente que la elección entre métodos alternativos se refiere exclusivamente a un producto no básico que no se requiera en la producción de ninguna otra mercancía no básica.
Puesto que los cambios de los procesos productivos que conciernen exclusivamente a tal tipo de productos no tienen consecuencias sobre los precios relativos de los demás ni sobre la tasa de beneficios máxima del sistema, las dos técnicas sólo difieren en el precio del producto considerado. Es entonces posible, rebus sic stantibus, comparar únicamente los procesos alternativos.
Por ejemplo, si para producir la mercancía no básica 2 se conocen dos métodos alternativos, a los que llamaremos I y II, el uso alternativo de uno de estos dos métodos de producción implica para la mercancía 2 uno de los dos costos de producción alternativos,
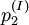 e
e  , que se obtienen así:
, que se obtienen así:
donde los precios del sistema económico considerado se expresan en términos de cualquier numerario.En este caso están dados:
. las cantidades producidas y utilizadas como medios de producción de las n mercancías para las dos técnicas alternativas:
. los precios de todas las demás mercancías n-1 y el salario unitario (o la tasa de beneficios si el salario fuera la variable exógena).
Técnicas de producción alternativas de mercancías no básicas en el caso de producción simple.El problema de la elección del método de producción de la mercancía 2 se reduce entonces a la simple comparación de los dos precios y a elegir el método que implica el menos precio, es decir, el menor costo. Esta elección depende, naturalmente, de una tasa de beneficios (salarios) dada. Y podría variar si se adopatara una tasa diferente. Sabemos, de hecho, que con la variación de la tasa de beneficios varían todos los precios y el salario unitario. Además a un aumento progresivo (o a una disminución progresiva) de la tasa de beneficios no seguirá siempre un aumento o una disminución del precio de la mercancía producida con un método con respecto al precio de esa misma mercancía producida con otro método; de modo que podrá haber casos en los que el precio de la mercancía 2 producida con el proceso I, con respecto al precio de la mercancía 2 producida con el proceso II, aumente en cierto rango de variación de la variable, para luego disminuir o permanecer constante (la gráfica muestra uno de los casos posibles).
Las tasas de beneficios correspondientes a los puntos de intersección de las curvas de precios representan puntos de cambio de técnica o, más simplemente, puntos de desplazamiento (en la figura
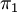 e
e 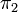 ). En estos puntos individuales de la tasa de beneficios es indiferente adoptar un método de producción u otro, porque los precios de las mercancías son iguales (
). En estos puntos individuales de la tasa de beneficios es indiferente adoptar un método de producción u otro, porque los precios de las mercancías son iguales (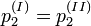 ).
).
Los razonamientos que se han presentado hasta aquí son independientes del tipo de numerario que utiliza el sistema de precios. La modificación del numerario sólo modifica la forma de todas las curvas, manteniendo sin embargo la invariancia de los puntos de cambio.Las elecciones de técnica para las mercancías básicas
El problema se complica cuando la elección entre métodos alternativos concierne a un producto básico. En efecto, en el caso de los productos básicos, que entran directamente o indirectamente en la producción de todas las mercancías, el cambio de un método de producción en la industria individual tiene efectos que se extienden a todo el sistema económico. El problema de la elección tecnológica para las mercancías básicas no se puede entonces resolver simplemente mediante la comparación de los precios alternativos como es posible hacer en el caso de las mercancías no básicas.
En tales circunstancias parece faltar una base común para poder comparar los dos métodos. En efecto, según se utilice uno u otro método, estaremos en uno u otro sistema económico, y a cada tasa de beneficios dada corresponderá, en cada sistema, un salario diferente, anque expresado en términos de la misma mercancía, y un sistema de precios relativos diferente; de modo que la comparación entre los precios de la mercancía producida según los dos métodos carece de sentido (Sraffa, 1960, p. 104).
Sin embargo, señala Sraffa, en los niveles de la tasa de beneficios que corresponden a los puntos de intersección de los dos métodos, al ser idéntico el precio de la mercancía básica producida con los dos métodos, los dos sistemas económicos presentarán la misma estructura de precios relativos y el mismo salario.[4]
Al final, luego de hacer posible la comparación de los dos métodos alternativos dentro del mismo sistema, también en aquellos niveles de la tasa de beneficios que los hacen incompatibles, Sraffa supone que dichos métodos producen dos mercancías distintas que, al poderse considerar idénticas para todos los usos básicos posibles, no son sustituibles en los usos no básicos, La consecuencia de dicha suposición es que, mientras que en los usos básicos la elección recaerá en el método que es más conveniente para toda tasa de beneficios dada, el otro método encontrará aplicación en los usos no básicos.
Llamemos entonces sistema I al sistema económico en el que el primer método se utiliza para los usos básicos y sistema II a aquel en que se utiliza el segundo método para tales usos. Suponiendo ahora que la tasa de beneficios máxima del sistema I es más alta que la del sistema II (
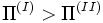 ), a las tasas de beneficios comprendidas entre esos máximos ((
), a las tasas de beneficios comprendidas entre esos máximos ((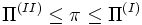 ) ) el método I sería el único posible para la producción del producto básico, y a fortiori el más conveniente, puesto que para esos valores de la tasa de beneficios el sistema II tendría un salario nulo o negativo. A medida que la tasa de beneficios disminuye, cualquier variación en el orden de conveniencia de los dos métodos debe “cumplirse igualmente en ambos sistemas, puesto que implica pasar por un punto de intersección, y tales puntos son comunes a ambos sistemas”. Ahora bien, a lo largo de la curva de variación de la tasa de beneficios puede haber más intersecciones entre los precios resultantes de ambos métodos, de modo que se presentarán otras tantas variaciones hacia delante y hacia atrás en el orden de conveniencia de estos métodos y, por consiguiente, de pasos de un sistema al otro.
) ) el método I sería el único posible para la producción del producto básico, y a fortiori el más conveniente, puesto que para esos valores de la tasa de beneficios el sistema II tendría un salario nulo o negativo. A medida que la tasa de beneficios disminuye, cualquier variación en el orden de conveniencia de los dos métodos debe “cumplirse igualmente en ambos sistemas, puesto que implica pasar por un punto de intersección, y tales puntos son comunes a ambos sistemas”. Ahora bien, a lo largo de la curva de variación de la tasa de beneficios puede haber más intersecciones entre los precios resultantes de ambos métodos, de modo que se presentarán otras tantas variaciones hacia delante y hacia atrás en el orden de conveniencia de estos métodos y, por consiguiente, de pasos de un sistema al otro.En vista de esta posibilidad –concluye Sraffa– no se puede afirmar (en contra de lo que se podría esperar) que en general, entre dos métodos de producción de una misma mercancía, el que corresponde al sistema patrón con una proporción más alta entre producto y medios de producción (en la práctica, el sistema económico con la tasa de beneficios máxima más elevada) es el más conveniente cuando la tasa de beneficios es relativamente alta y el menos conveniente cuando es relativamente baja.
Este análisis se puede extender al caso en que hay más de dos métodos alternativos, y no sólo para uno de los productos sino para cada uno de ellos. En ese caso, cuando aumenta la tasa de beneficios habrá una “rápida sucesión de desplazamientos de los métodos de producción de una u otra de las mercancías”.
Cabe señalar, por último, que no obstante que en cada desplazamiento del método de producción la relación patrón y la tasa máxima de beneficios del sistema pueden aumentar o disminuir, a cada aumento de la tasa de beneficios, qualquiera que sea la mercancía elegida como numerario, seguirá siempre una disminución del salario. Esto ocurre porque las variaciones de la tasa de beneficios y del salario que se presentan sin que haya un cambio de método, se presentan en el mismo sistema; mientras que cuando se pasa de un método a otro, esto sucede en niveles dados del salario y de la tasa de beneficios, sin que implique de por sí una variación de las variables distributivas.
Referencias bibliográficas
• Pasinetti, Luigi (1989), Lectures on the Theory of Production, Bologna, El Mulino.
• [[Sraffa, Piero]] (1960), Producción de mercancías por medio de mercancías,Oikos-Tau, Barcelona.
• Salvadori, N. y Kurz, H.D. (1995), Theory of Production, Cambridge, Cambridge University Press.
Términos relacionados
• Piero Sraffa • David Ricardo • Economía clásica
Notas
1. El hecho de que el salario unitario se mida en términos de la mercancía patrón no implica que se gaste en la compra de la mercancía patrón; sólo implica que las mercancías que los trabajadores compren (cualesquiera que sean) tendrán un valor igual al valor de la cantidad de mercancía patrón que representa el salario.
2. Puesto que el producto neto efectivo es, en generale, diferente del producto neto patrón, la parte del producto neto efectivo que queda para los beneficios no será igual ni a 1/4 del producto neto efectivo (dado que los 3/4 que se restan se refieren al producto neto patrón) ni a 1/4 del producto neto patrón (dado que los 3/4 del mismo se han restado del producto neto efectivo); y sin embargo su relación con los medios de producción será del 5%.
3. Este es un caso aberrante que Sraffa discute por aparte, en uno de los apéndices de Producción. De hecho, para ese valor particular de R todos los precios serían cero en términos de la mercancía no básica de la que se trata.
4. El salario se puede expresar en términos de cualquier mercancía. Cabe señalar, sin embargo, que, siendo diferentes la tasa de beneficios máxima y la relación patrón en los dos sistemas, y siendo diferentes en uno de los procesos relacionados con una mercancía básica, el producto neto patrón será diferente. Por consiguiente, el salario, aunque igual en términos de mercancía, corresponderá a diferentes proporciones de los productos netos patrón respectivos de los dos sistemas.
Enlaces externos
- Perfil de Piero Sraffa en el sito History of Economic Thought
- Página de los Archivos en el Trinity College de Cambridge. Contiene un catálogo en línea de sus documentos personales y profesionales
historia del pensamiento económico
Esto es una traducción aproximada del excelente texto original: http://it.wikipedia.org/wiki/Produzione_di_merci_a_mezzo_di_merci
Categorías: Teoría económica | Historia económica | Libros de economía | Economía marxista
Wikimedia foundation. 2010.

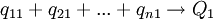
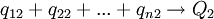

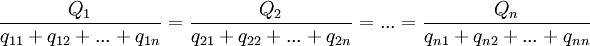
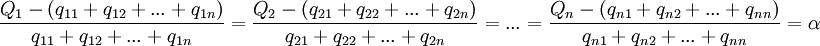
![(1-\omega)[Q_1-(q_{11}+q_{12}+ \ldots +q_{1n}) + Q_2-(q_{21}+q_{22}+ \ldots +q_{2n}) + \ldots + Q_n-(q_{n1}+q_{n2}+ \ldots +q_{nn})]](/pictures/eswiki/48/0dbc9fcc98324574b5a0465f12b21723.png)