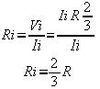Contenido 1 medición de Resistencias de Alto Valor 2 medición de una resistencia de Alto Valor por Método de CBM 3 Véase también 4 Referencia:

medición de Resistencias de Alto Valor

Para la medición de una resistencia de más de 10 MΩ se puede utilizar varios métodos (por ej: CBM, puente de Wheatstone, etc) pero sin importar el método que se aplique, el problema que siempre aparece es que lo que en realidad se esta midiendo es el paralelo entre R y RF.

Para solucionar este problema se ideo el colocar un tercer terminal a la resistencia.

Las resistencias de 3 terminales están conformadas por el resistor propiamente dicho con el dieléctrico que lo envuelve y luego se le agrega una malla metálica, que envuelve al dieléctrico, de donde sale el tercer terminal.

Si bien la malla metálica no elimina las corrientes de fugas (ni siquiera las reduce), la función que cumple es la de darnos la posibilidad de formar un nuevo circuito donde RF este conectada de tal manera de poder despreciarla. ¿Como es esto? Pues bien, para poder entenderlo es mejor verlo en un ejemplo, por lo que a continuación se lo va a explicar con el método de CBM.

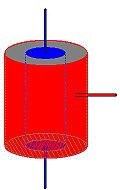
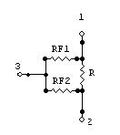
La figura de la izquierda muestra un resistencia de 3 terminales donde la parte azul representa la resistencia propiamente dicha, la parte gris es el dieléctrico que cubre a la resistencia, y la parte roja es el metal que envuelve a todo el resistor y de donde sale el 3er terminal. La figura de la derecha muestra el modelo circuital para una resistencia de 3 terminales, donde RF1 y RF2 representan las corrientes de fuga entre el resistor y la malla metálica que lo envuelve.

Un ejemplo de una resistencia de 3 terminales es el anillo de guarda que se usa tanto en solido como en liquidos.

medición de una resistencia de Alto Valor por Método de CBM

El método de corriente Bien Medida (CBM) es un método de medición indirecta principalmente aplicable al medir resistencias de muy alto valor, donde su error de método es mínimo El circuito del método CBM es el siguiente:

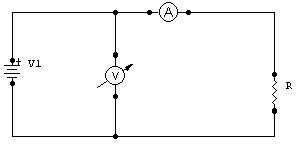
Ahora, si dejamos de considerar ideales los instrumentos, no quedaría de la siguiente forma:

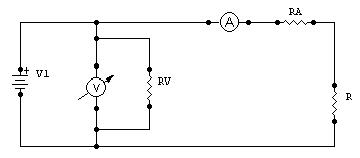
Donde aparecen RA (impedancia interna del amperímetro) y RV (impedancia interna del voltímetro). Estas son las responsables del error de método cometido en este método, ya que si bien el amperímetro esta midiendo la corriente real que circula por R; el voltímetro esta midiendo en realidad la caída de tensión sobre la suma de R y RA.

=> Vi = Ii (R + RA)

Siendo que R>>RA => Vi ~ Ii . R , por lo que si se calcula el error de método, se puede ver que es menor cuanto mayor es el valor de R.

Ahora veamos que sucede cuando el valor de R es tan grande que se empieza a equiparar con el valor de su resistencia de fuga (RF). Para esto debemos aplicar el modelo anteriormente visto para resistencia altas.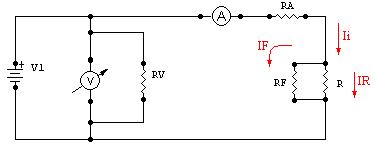

Como se puede ver en la figura, la corriente que indica el amperímetro ahora es en realidad la suma de la corriente del resistor (IR) mas la corriente de fuga del mismo (IF). Si bien esto es algo que sucede en todas las mediciones, para resistencias medias es totalmente despreciable; pero en este caso los valores de RF y R son similares por lo que IR también es similar a IF, introduciendo un error muy significativo a la medición Supongamos como ejemplo que RF = 2R. Si analizamos el circuito podemos deducir la siguiente ecuación:

y siendo que R//RF sigue siendo mucho mayor a RA, y siendo RF=2R, entonces:

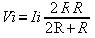
Resultando que la resistencia indicada va a ser 2/3 del valor real. Si bien uno pude pensar que sabiendo el valor de RF, uno puede corregir la indicación como cualquier otro error de método, justamente la dificultad se encuentra en que es muy difícil determinar con una exactitud aceptable el valor de RF. Esto se debe a que las corrientes de fuga varían no solo por el dieléctrico usado, sino también por las condiciones ambientales. Para evitar estos problemas es que aparecen las resistencias de 3 terminales, y lo que se hace para este caso es conectar el 3er terminal de la siguiente manera:

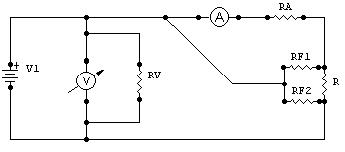
Como se puede ver, al conectar el 3er terminal de esta manera, termina quedando RF1 en paralelo al amperímetro y RF2 en paralelo al voltímetro Siendo que RF1 >>> RA, puedo despreciar RF1 sin temor a cometer un error significativo. Por otro lado, el que RF2 quede en paralelo al voltímetro no me implica ninguna variación en la medición ya que, indistintamente del valor de RF2 y RV, el voltímetro sigue midiendo la caída de tensión sobre )(R + RA). De este modo, si bien no eliminé ni disminuí el valor de las corrientes de fuga, si pude excluirlas de la medición de R.

Véase también

• resistor
• Resistencia eléctrica
• Modelo resistor real
• Resistencias de bajo valor
• Anillo de Guarda
• Implementación del Tercer Terminal sobre Líquidos

Referencia:

• Apuntes de Clase de Medidas Electrónicas I, curso R4052, Año 2009, UTN FRBA - Argentina.