- Teorema de euler para ecuaciones homogéneas de grado
-
Teorema de euler para ecuaciones homogéneas de grado
Teorema de Euler para ecuaciones homogéneas de grado, es un teorema que hace mención a cierta propiedad de igualdad matemática que cumplen las denominadas funciones homogéneas de grado.
Contenido
Enunciado del teorema
Si una función
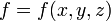es una función homogénea de grado n podemos afirmar que: 
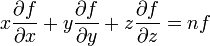, es decir, de manera más simplificada :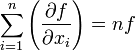 
Definición de función homogénea de grado / ecuación homogénea de grado
Una función
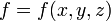se dice función homogénea de grado n 
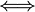para un valor arbitrario 
, 
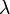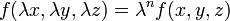
Demostración
La demostración directa consiste en partir de la definición admitida de función homogénea y derivar ambos términos con respecto a
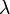. Es decir, la demostración es una consecución de los siguientes pasos:- Es una función homogénea, esto implica que
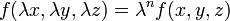
![d[f(\lambda x,\lambda y,\lambda z)]=\frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda x)}d(\lambda x) + \frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda y)}d(\lambda y)+ \frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda z)}d(\lambda z)](/pictures/eswiki/97/ac1240e52c2eb64b7e3bb76b98f37696.png)
![\frac{d[f(\lambda x,\lambda y,\lambda z)]}{d \lambda}=\frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda x)}\frac{d(\lambda x)}{d\lambda} + \frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda y)}\frac{d(\lambda y)}{d\lambda} + \frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda z)}\frac{d(\lambda z)}{d\lambda} = \frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda x)}x + \frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda y)}y + \frac{\partial f(\lambda x,\lambda y,\lambda z)}{\partial (\lambda z)}z](/pictures/eswiki/54/695d10c0df907be8002977662066049f.png)
- Por otro lado
![\frac{d[\lambda^n f(x,y,z)]}{d\lambda}=n\lambda^{n-1}f(x,y,z)](/pictures/eswiki/101/ec6c34795c41d92388325e9ecaf9bf98.png)
Es decir:
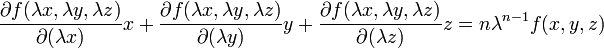
Puesto que lamba es un valor arbitrario podemos afirmar que con λ = 1 lo expuesto queda como
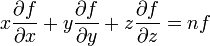que es el teorema de Euler.Aplicaciones del teorema
Aplicaciones en Física: Termodinámica
Si la función de estado termodinámica es:
- Homogénea de grado 1: función de variables extensivas :
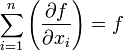
- Homogénea de grado 0: función de variables intensivas :
Bibliografía
- Curso de Termodinámica José Aguilar Peris
- Apuntes de la asignatura Fundamentos de termodinámica Grado de Física, Universidad de Santiago de Compostela, España
Categorías: Termodinámica | Principios y leyes físicas - Es una función homogénea, esto implica que
Wikimedia foundation. 2010.
