Autómata con pila

Autómata con pila: Autómata con pila

Saltar a navegación, búsqueda

Un autómata con pila o autómata de pila o autómata a pila o autómata apilador es un modelo matemático de un sistema que recibe una cadena constituida por símbolos de un alfabeto y determina si esa cadena pertenece al lenguaje que el autómata reconoce. El lenguaje que reconoce un autómata a pila pertenece al grupo de los lenguajes de contexto libre en la clasificación de la Jerarquía de Chomsky.

Definición formal

Formalmente, un autómata con pila puede ser descrito como una séptupla $M = (S,Σ,Γ,δ, s, Z, F)$ donde:

Σ y $Γ$ son alfabetos de entrada, de la cadena y de la pila respectivamente;

S un conjunto de estados;

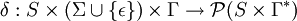
$\delta: S \times (\Sigma \cup \{\epsilon \} ) \times \Gamma \rightarrow \mathcal{P} ( S \times \Gamma^*)$

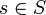$s \in S$ es el estado inicial;

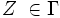$Z\ \in \Gamma$ es el símbolo inicial de la pila;

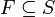$F \subseteq S$ es un conjunto de estados de aceptación o finales.

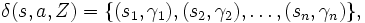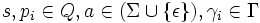La interpretación de $\delta (s, a, Z) = \{ (s_1, \gamma_1), (s_2, \gamma_2), \ldots, (s_n, \gamma_n) \},$ con $s, p_i \in Q, a \in (\Sigma \cup \{ \epsilon \} ), \gamma_i \in \Gamma$ es la siguiente:

Cuando el estado del autómata es $s$ , el símbolo que la cabeza lectora está inspeccionando en ese momento es $a$ , y en la cima de la pila nos encontramos el símbolo $Z$ , se realizan las siguientes acciones:

Si 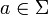$a \in \Sigma$ , es decir no es la palabra vacía, se avanza una posición la cabeza lectora para inspeccionar el siguiente símbolo.

Se elimina el símbolo Z de la pila del autómata.

Se selecciona un par $(p i,γ i)$ de entre los existentes en la definición de $δ(s, A, Z)$ , la función de transición del autómata.

Se apila la cadena 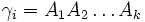$\gamma_i = A_1 A_2 \ldots A_k$ en la pila del autómata, quedando el símbolo $A 1$ en la cima de la pila.

Se cambia el control del autómata al estado $p i$ .

Ejemplo

Sea el siguiente lenguaje libre del contexto 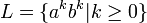$L = \{a^kb^k | k \ge 0 \}$ ; formado por las cadenas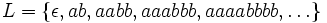 $L = \{ \epsilon , ab, aabb, aaabbb, aaaabbbb, \ldots \}$

Dicho lenguaje puede ser reconocido por el siguiente autómata con pila:

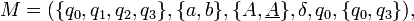
$M = (\{q_0, q_1, q_2, q_3\}, \{a,b\}, \{A,\underline{A}\}, \delta, q_0, \{q_0, q_3 \}),$

donde las transiciones son:

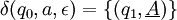
$\delta(q_0, a, \epsilon) = \{(q_1, \underline{A})\}$

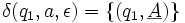
$\delta(q_1, a, \epsilon) = \{(q_1, \underline{A})\}$

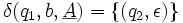
$\delta(q_1, b, \underline{A}) = \{(q_2, \epsilon)\}$

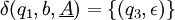
$\delta(q_1, b, \underline{A}) = \{(q_3, \epsilon)\}$

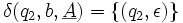
$\delta(q_2, b, \underline{A}) = \{(q_2, \epsilon)\}$

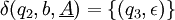
$\delta(q_2, b, \underline{A}) = \{(q_3, \epsilon)\}$

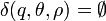$\delta(q, \theta, \rho) = \empty$ para cualquier $(q,θ,ρ)$

El significado de las transiciones puede ser explicado analizando la primera transición:

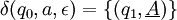
$\delta(q_0, a, \epsilon) = \{(q_1, \underline{A})\}$

donde $q 0$ es el estado actual, $a$ es el símbolo en la entrada y $ε$ se extrae de la cima de la pila. Entonces, el estado del automata cambia a $q 1$ y el símbolo 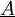$\underline{A}$ se coloca en la cima de la pila.

La idea del funcionamiento del autómata es que al ir leyendo los diferentes símbolos a, estos pasan a la pila en forma de símbolos A. Al aparecer el primer símbolo b en la entrada, se comienza el proceso de desapilado, de forma que coincida el número de símbolos b leídos con el número de símbolos A que aparecen en la pila.

Autómata determinista

Nótese que, a diferencia de un autómata finito o una máquina de Turing, la definición básica de un autómata con pila es de naturaleza no determinista, pues la clase de los autómatas con pila deterministas, a diferencia de lo que ocurría con aquellos modelos, tiene una potencia descriptiva estrictamente menor. Para calificar a un autómata con pila como determinista deben darse dos circunstancias; en primer lugar, por supuesto, que en la definición de cada componente de la función de transición existan un único elemento lo que da la naturaleza determinista. Pero eso no es suficiente, pues además puede darse la circunstancia de que el autómata esté en el estado $s$ y en la pila aparezca el símbolo $s Z$ , entonces, si existe una definición de transición posible para algún símbolo cualquiera $a$ del alfabeto de entrada, pero, además existe otra alternativa para la palabra vacía $ε$ , también esto es una forma de no determinismo, pues podemos optar entre leer un símbolo o no hacerlo. Por eso, en autómata determinista no debe existir transición posible con lectura de símbolo si puede hacerse sin ella, ni al contrario.

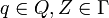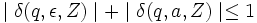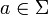Para cada $q \in Q, Z \in \Gamma$ , se dé que: $\mid \delta(q,\epsilon,Z)\mid + \mid \delta(q,a,Z)\mid \le 1$ , para cada $a \in \Sigma$

Obtenido de "Aut%C3%B3mata con pila"

Categoría: Lenguajes formales

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

Autómata — Saltar a navegación, búsqueda Autómata del griego automatos (αὐτόματος) que significa espontáneo o con movimiento propio, puede referirse a: Autómata programable: Equipo electrónico programable en lenguaje no informático y diseñado para controlar … Wikipedia Español
Autómata programable — Saltar a navegación, búsqueda En electrónica un autómata es un sistema secuencial, aunque en ocasiones la palabra es utilizada también para referirse a un robot. Puede definirse como un equipo electrónico programable en lenguaje no informático y… … Wikipedia Español
Autómata finito — Un autómata finito (AF) o máquina de estado finito es un modelo matemático que realiza cómputos en forma automática sobre una entrada para producir una salida. Este modelo está conformado por un alfabeto, un conjunto de estados y un conjunto de… … Wikipedia Español
Máquina de pila — Una máquina de pila es un modelo computacional en el cual la memoria de la computadora toma la forma de una o más pilas. El término también se refiere a un computador real implementando o simulando una máquina de pila idealizada. Adicionalmente,… … Wikipedia Español
Teoría de autómatas — La teoría de autómatas es una rama de las ciencias de la computación que estudia las máquinas abstractas y los problemas que éstas son capaces de resolver. La teoría de autómatas está estrechamente relacionada con la teoría del lenguaje formal ya … Wikipedia Español
Notación polaca — Notación polaca. La notación polaca, también conocida como notación de prefijo o notación prefija, es una forma de notación para la lógica, la aritmética, y el álgebra. Su característica distintiva es que coloca los operadores a la izquierda de… … Wikipedia Español
Jerarquía de Chomsky — Noam Chomsky. En lingüística la jerarquía de Chomsky es una clasificación jerárquica de distintos tipos de gramáticas formales que generan lenguajes formales. Esta jerarquía fue descrita por Noam Chomsky en 1956. Contenido … Wikipedia Español
Máquina de Turing — Para otros usos de este término, véase Turing (desambiguación). Una máquina de Turing (MT) es un modelo computacional que realiza una lectura/escritura de manera automática sobre una entrada llamada cinta, generando una salida en esta misma. Este … Wikipedia Español
Estado (informática) — Saltar a navegación, búsqueda En Ciencias de la computación y en Teoría de autómatas, un estado es una configuración única de información en un programa o máquina. Esto es un concepto que ocasionalmente se ha extendido en varias formas de… … Wikipedia Español
Autómatas linealmente acotados — Saltar a navegación, búsqueda Un autómata linealmente acotado, abreviadamente LBA (del inglés, Linear Bounded Automaton), es un autómata similar a una máquina de Turing no determinista. Contenido 1 Historia 2 Autómatas lineales … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Autómata con pila

Autómata con pila

Definición formal

Ejemplo

Autómata determinista

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Autómata con pila

Autómata con pila

Definición formal

Ejemplo

Autómata determinista

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo