Algoritmo de navegación

Este artículo o sección sobre informática necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 18 de agosto de 2011. También puedes ayudar wikificando otros artículos.

Los Algoritmos de navegación son la quintaesencia del software ejecutable en calculadoras portátiles o en PDA como ayuda al arte de la navegación, este artículo intenta describir tanto los algoritmos como el software para "PC-PDA " que implementan los diferentes procedimientos de cálculo para la navegación.

La potencia de cálculo obtenida por los lenguajes: básico, "C", java, etc .., de las calculadoras portátiles o de las PDA, ​​ha hecho que se pudieran desarrollar programas que permiten calcular la posición sin necesidad de tablas, de hecho tienen unas tablas básicas con los factores de corrección para cada año y calculan los valores "al vuelo" en tiempo de ejecución.

Comparación entre los métodos de cálculo manuales y el uso de calculadoras o similares

• Los métodos tradicionales necesitan tablas náuticas (que hay que poner al día) voluminosas y caros, lápiz y papel y tiempo de cálculo. Y siguen algoritmos de trabajo.
• Las calculadoras (y similares) no necesitan libros (tienen las tablas y efemérides integradas) y, con unos algoritmos propios, permiten el cálculo rápido y sin errores de los problemas de navegación.

Tipos de algoritmos

• Navegación general Distancia, demora, angle horizontal, IALA, rumbos, navegación loxodrómica, navegación ortodrómica, partes de meridiano, meteorología náutica, mareas ...
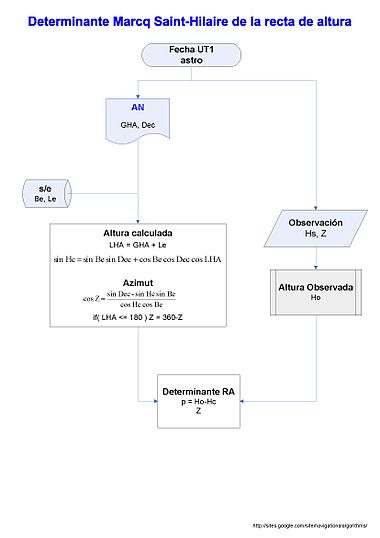
• Navegación Astronómica : Reducción de observaciones, círculos y rectas de altura, posición observada, RA, Gha, Dec ..
• Software shareware PC-PDA : Almanaque náutico, navegación, declinación magnética, corrección de la altura, ...

Programas para la navegación general

Programas sobre la carta náutica, rumbos, navegación costera y balizas, publicaciones náuticas. La sección de navegación astronómica incluye la resolución del el triangle de posición, la utilidad de una recta de altura, el reconocimiento de astros y el determinante de la recta de altura Además de otros temas de interés en náutica: mareas, cinemática naval, meteorología y huracanes, y oceanografía.

Toda medida del rumbo efectuada con un compás magnético o brújula debe ser corregida debido a la declinación magnética o variación local.

Coordenadas astronómicas

Correcciones Hs..

Obtención de la recta de altura Marcq St. Hilaire.

Subrutina de conversión de coordenadas

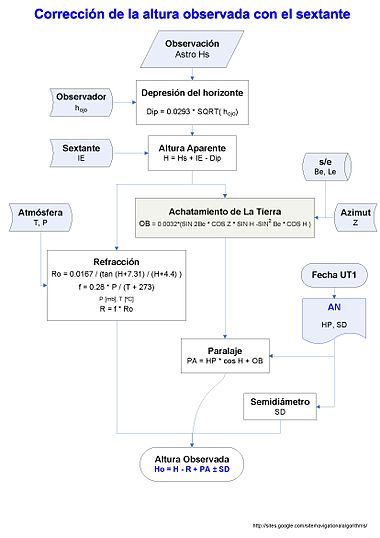
sub Rectang2Polar (a () as double, b () as double) static
 '----- Subprograma para convertir un vector de estado coord.cartesianes
 '----- En vector de estado en coord.polars.
 '----- De entrada: vector de estado en coord.cartesianes
 '----- De salida: vector de estado en coord.polars.
 '----- NOTA: El vector de velocidad polar es el de la velocidad total,
 '----- Corregido por el efecto de la latitud.
 '------------------------------------------------- ------------------------
 mar x as double
 mar y as double
 mar z as double
 mar x_dot as double
 mar y_dot as double
 mar z_dot as double
 mar rho as double
 mar r as double
 mar lambda as double
 mar beta as double
 mar lambda_dot as double
 mar beta_dot as double
 mar r_dot as double
 x = a (1)
 y = a (2)
 z = a (3)
 x_dot = a (4)
 y_dot = a (5)
 z_dot = a (6)
 rho = sqr (x * x+y * y)
 r = sqr (rho * rho+z * z)
 lambda = atan2 (y, x)
 beta = atan2 (z, rho)
 if (z <0 #) then beta = beta - TWOPI
 yf rho = 0 # then
   lambda_dot = 0 #
     beta_dot = 0 #
 else
   lambda_dot = (x * y_dot - y * x_dot)/(rho * rho)
     beta_dot = (z_dot * rho * rho - z * (x * x_dot+_
                  y * y_dot))/(r * r * rho)
 end if
 r_dot = (x * x_dot+y * y_dot+z * z_dot)/r
 '----- Componentes del vector de posición
 b (1) = lambda
 if b (1)> = TWOPI then b (1) = b (1) - TWOPI
 b (2) = beta
 b (3) = r
 '----- Componentes del vector velocidad total
 b (4) = r * lambda_dot * cuerpo (beta)
 b (5) = r * beta_dot
 b (6) = r_dot
end sub

Programas para la navegación astronómica

Los algoritmos sobre navegación avanzada incluyen pilotaje y navegación astronómica: loxodromia y ortodrómica. Corrección de la altura del sextante. Posición astronómica con calculadora, Plantilla y Carta mercatoria en blanco. Posición por 2 Rectas de Altura. Posición a partir de n Rectas de Altura. Ecuación vectorial del Círculo de Altura. Posición para solución vectorial a partir de dos observaciones. Posición por Círculos de Altura: solución matricial. Y artículos relacionados con procedimientos antiguos como la obtención de la latitud por la estrella polar, la meridiana, el método de las distancias lunares, etc.

Programas de Cálculo Astronómico

Resuelven el problema de calcular la posición a partir de observaciones de astros efectuadas con el sextante en Navegación Astronómica.

Implementación de algoritmos:

• Para n <2 observaciones
  • An analytical solution of the two star sight problem of celestial navegación, James A. Van Allen.^[1]
  • Vector Solution for the Intersection of two Circles of Equal Altitude. Andrés Ruiz.^[2]
• Para n> = 2 observaciones
  • DeWit/USNO Nautical Almanac/Compac Fecha, Least squares algorithm for n LOPS
  • Kaplan algorithm, USNO.^[3]
• Para n> = 8 observaciones, da además la solución para el rumbo y la velocidad de fondo.

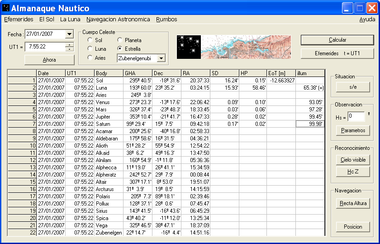
Programas para el "Almanaque Náutico"

Ejemplo Programa Almanaque Náutico

Calculan las efemérides de los astros usados ​​en navegación

• Gha - angle Horario respecto Greenwich
• Dic - Declinación
• SD - Semidiàmetre
• HP - paralaje Horizontal

Véase también

• Historia de la navegación astronómica
• Almanaque náutico
• Sextante
• Recta de altura

Referencias

Enlaces externos

• Vector Solution for the Intersection of Two Circles of Equal Altitude, Andrés Ruiz.
• Journal of Navigation (en inglés)
• The Institute of Navigation (en inglés)
• Navigational Algorithms