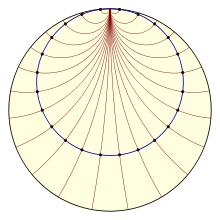
Horociclo

Disco de Poincaré.
En azul: horociclo.
En rojo: normales que convergen asintóticamente al punto superior central.

En geometría hiperbólica, un horociclo (también llamado oriciclo u oricírculo) del griego όριο + κύκλος, es una curva cuyas normales convergen asintóticamente. Es el ejemplo bidimensional de de una horoesfera (u orisfera).

Un horociclo también puede ser descrito como el límite de los círculos que comparten una tangente en un punto dado, cuando sus radios tienden a infinito. En geometría euclidiana ordinaria, una tal «círculo de radio infinito» sería una línea recta, pero en geometría hiperbólica ésta se curva. Del lado convexo el horociclo es aproximado por hiperciclos cuyas distancias tienden a infinito.

En el modelo del disco de Poincaré del plano hiperbólico, los horociclos se representan por círculos tangentes al círculo exterior. En el semiplano de Poincaré, los horociclos se representan por círculos tangentes a la línea exterior «y» por líneas paralelas a la línea exterior. En el modelo del hiperboloide, se representan por intersecciones del hiperboloide con planos cuya normal se encuentra sobre el cono asintótico.

Referencias

• H.S.M. Coxeter (1961) Introduction to Geometry, §16.6: "Circles, horocycles, and equidistant curves", page 300,1, John Wiley & Sons.