Modelo de dos dobletes de Higgs

Modelo de dos dobletes de Higgs
Una simulación del detector CMS de LHC, mostrando cómo se prevé que sean las trazas del bosón de Higgs.
Espectro de Higgses: los grados de libertad de ambos dobletes de Higgs se combinan según la figura para formar tres bosones neutros y dos cargados.

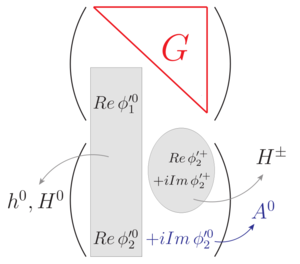
Los modelos con dos dobletes de Higgs (2HDM) son una extensión del modelo estándar en la que el sector de Higgs está compuesto por dos dobletes de SU(2)L, en lugar de uno solo.[1] Estos dobletes interacción a través de un potencial que rompe espontáneamente la simetría electrodébil al grupo U(1) de carga eléctrica, dando lugar a tres bosones de Goldstone y a cinco bosones físicos (dos cargados y tres neutros). Nótese la diferencia con el modelo estándar, en la que solo sobrevive un grado de libertad físico: el bosón de Higgs.


Introducción

El mecanismo por el que se rompe la simetría electrodébil no es bien conocido. El modelo estándar lo implementa de la forma más sencilla posible, introduciendo un nuevo doblete escalar, cuyos grados de libertad interaccionan a través de un potencial cuyo mínimo es degenerado, causando que este doblete pueda adquirir un valor esperado en el vacío no nulo, rompiendo la simetría. Los modelos con dos dobletes de Higgs son la extensión más simple que se puede hacer, que consiste en introducir un segundo doblete escalar.

Desarrollo matemático

El sector de Higgs de los 2HDM está compuesto por dos dobletes complejos de SU(2)L, \phi_1 y \phi_2 de hipercarga 1 / 2, que interacción entre sí a través del potencial más general, invariante gauge, renormalizable e invariante bajo la simetría \phi_1\rightarrow -\phi_1 (salvo términos de orden dos):

V(\phi_1, \phi_2) = \lambda_1(\phi_1^\dagger \phi_1 - v_1^2)^2 + \lambda_2 (\phi_2^\dagger \phi_2 - v_2^2)^2 + \lambda_3\left[(\phi_1^\dagger \phi_1-v_1^2) + (\phi_2^\dagger \phi_2 - v_2^2)\right]^2
+\lambda_4\left[(\phi_1^\dagger \phi_1)(\phi_2^\dagger\phi_2) - (\phi_1^\dagger \phi_2)(\phi_2^\dagger \phi_1)\right]+ \lambda_5\left[\text{Re}(\phi_1^\dagger \phi_2) - v_1 v_2 \cos{\epsilon}\right]^2
+\lambda_6\left[\text{Im}(\phi_1^\dagger \phi_2)-v_1 v_2 \sin{\epsilon}\right]^2.

El mínimo de este potencial está degenerado. Cuando \phi_1 y \phi_2 toman un valor esperado en el vacío no nulo, se rompe la simetría gauge al grupo de carga eléctrica:

\phi_1 = \begin{bmatrix} 0 \\ v_1 \end{bmatrix},\qquad \phi_2 = \begin{bmatrix} 0 \\ v_2 e^{i\epsilon} \end{bmatrix}, \qquad \epsilon << 1.

Un parámetro ε distinto de cero introduce una violación espontánea de CP. Asimismo, se ha sugerido recientemente[2] que la masa de los neutrinos podría explicarse con un valor de v1 muy pequeño. En lo que sigue, suponemos que ε es exactamente cero. En ese caso, se puede realizar un giro en el espacio bidimensional generado por ambos dobletes, de tal forma que una combinación adquiere valor esperado, mientras que la otra no. Es decir, el primero de estos campos gurados se comporta como el Higgs del modelo estándar, rompiendo la simetría; mientras que el otro, al no adquirir valor esperando, no la rompe. Los grados de libertad no físicos (los Goldstone), por tanto, han de pertenecer al primero de ellos.

\begin{align} \phi_1'& = \cos{\beta}\, \phi_1 + \sin{\beta}\,\phi_2,\qquad\phi_2' & = -\sin{\beta}\,\phi_1 + \cos{\beta}\,\phi_2, \qquad \tan{\beta} = \dfrac{v_2}{v_1}.\\ \end{align}
\langle \phi_1' \rangle = \left(\begin{array}{c} 0\\ \sqrt{v_1^2+v_2^2} \end{array}\right),\qquad \langle \phi_2' \rangle = \left(\begin{array}{c} 0\\ 0 \end{array}\right).

Referencias

  1. ↑ John F. Gunion, Howard E. Haber, Gordon L. Kane, Sally Dawson (1990). . Addison-Wesley, Menlo-Park. SCIPP-89-13.
  2. ↑ Shainen M. Davidson and Heather E. Logan (2009). «Dirac neutrinos from a second Higgs doublet». arXiv:0906.3335v2.

Wikimedia foundation. 2010.

Игры ⚽ Нужно решить контрольную?

Mira otros diccionarios:

  • Mecanismo de Higgs — El mecanismo de Higgs, ideado por Peter Higgs entre otros, es uno de los mecanismos posibles para producir la ruptura espontánea de simetría electrodébil en una Teoría Gauge invariante. Permitió establecer, la unificación entre la teoría… …   Wikipedia Español

  • Technicolor (física) — Las teorías Technicolor son modelos de física Más allá del modelo estándar que nos llevan a la ruptura de la simetría electrodébil, el mecanismo por el cual las partículas elementales adquieren masa. Las primeras teorías technicolor se basaron en …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”