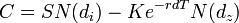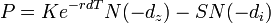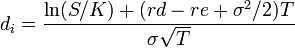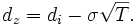Black-Scholes

Black-Scholes

Black-Scholes

En 1973, Robert C. Merton publicó "Theory of Rational Option Pricing", en él hacia referencia a un modelo matemático que Fisher Black y Myron Scholes habían desarrollado.

A este modelo lo denominó Black-Scholes y fue empleado para estimar el valor hoy de una opción europea para la compra (Call), o venta (Put), de acciones en una fecha futura, que posteriormente, o se desarrolló para opciones sobre acciones que producen dividendos, y luego se adoptó para opciones europeas, americanas, y de monedas.

En 1997, Merton y Scholes recibieron el Premio Nobel en Economía por su trabajo; Black, el otro creador de la fórmula, falleció en 1995.

El modelo concluye en que:

C = S N(d_i) - Ke^{-rdT}N(d_z) \,
P = K e^{-rdT}N(-d_z) - S N(-d_i) \,


Donde:


d_i = \frac{\ln(S/K) + (rd -re + \sigma^2/2) T}{\sigma\sqrt{T}}
d_z = d_i - \sigma\sqrt{T}.


Definiendo:

  • C es el valor de una opción de compra, opción europea.
  • P es el valor de una opción de venta, opción europea.
  • S es la tasa a la vista de la moneda que constituye el objeto de la opción.
  • K es el precio marcado en la opción (Strike price).
  • T es el tiempo expresado en años que aun faltan por transcurrir en la opción.
  • rd es la tasa de interés doméstica.
  • re es la tasa de interés extranjera.
  • σ Es la desviación Standard de los cambios proporcionales en las tasas de cambio.
  • N es la función de distribución acumulativa de la distribución normal.
  • N (di) y N (dz) son los valores de las probabilidades de los valores de di y dz tomadas de las tablas de la distribución normal.

Enlaces externos

Obtenido de "Black-Scholes"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Black–Scholes — The Black–Scholes model (pronounced /ˌblæk ˈʃoʊlz/[1]) is a mathematical model of a financial market containing certain derivative investment instruments. From the model, one can deduce the Black–Scholes formula, which gives the price of European …   Wikipedia

  • Black-Scholes — Das Black Scholes Modell ist ein finanzmathematisches Modell zur Bewertung von Finanzoptionen, das von Fischer Black und Myron Samuel Scholes 1973 (nach zweimaliger Ablehnung durch renommierte Zeitschriften) veröffentlicht wurde und als ein… …   Deutsch Wikipedia

  • Black-Scholes — Modèle Black Scholes Le terme de Black Scholes est utilisé pour désigner trois concepts très proches : le modèle Black Scholes est un modèle mathématique du marché pour une action, dans lequel le prix de l action est un processus… …   Wikipédia en Français

  • Black scholes — Modèle Black Scholes Le terme de Black Scholes est utilisé pour désigner trois concepts très proches : le modèle Black Scholes est un modèle mathématique du marché pour une action, dans lequel le prix de l action est un processus… …   Wikipédia en Français

  • Black-Scholes model — A financial option pricing model to calculate the expected value of share based payments using variables such as dividend yield, exercise period, exercise price, market price, risk free rate of return and share price volatility. The model assumes …   Law dictionary

  • Black-Scholes-Formel — Das Black Scholes Modell ist ein finanzmathematisches Modell zur Bewertung von Finanzoptionen, das von Fischer Black und Myron Samuel Scholes 1973 (nach zweimaliger Ablehnung durch renommierte Zeitschriften) veröffentlicht wurde und als ein… …   Deutsch Wikipedia

  • Black-Scholes-Modell — Das Black Scholes Modell (gesprochen ˌblæk ˈʃoʊlz[1]) ist ein finanzmathematisches Modell zur Bewertung von Finanzoptionen, das von Fischer Black und Myron Samuel Scholes 1973 (nach zweimaliger Ablehnung durch renommierte Zeitschriften)… …   Deutsch Wikipedia

  • Black Scholes Model — A model of price variation over time of financial instruments such as stocks that can, among other things, be used to determine the price of a European call option. The model assumes that the price of heavily traded assets follow a geometric… …   Investment dictionary

  • Black-Scholes option pricing model — A model for pricing call options based on arbitrage arguments. Uses the stock price, the exercise price, the risk free interest rate, the time to expiration, and the expected standard deviation of the stock return. Developed by Fischer Black and… …   Financial and business terms

  • Black Scholes — The name of a theoretical option pricing model in widespread use in the market place. Named after Fischer Black and Myron Scholes who first developed the model. Dresdner Kleinwort Wasserstein financial glossary …   Financial and business terms

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”