Brian Greene en Harvard

Brian Greene (nacido el 9 de febrero de 1963, Nueva York) es un físico estadounidense y uno de los mayores defensores de la teoría de cuerdas.

Vida

Brian Greene es profesor en la Universidad de Columbia desde el año 1996. Greene fue un prodigio de las matemáticas. A la temprana edad de 5 años ya era capaz de multiplicar cifras de 30 dígitos^{[cita requerida]}. Su nivel en matemáticas era tan alto, que a los 12 años recibió clases de un profesor de la Universidad Columbia, ya que había sobrepasado con creces el nivel el matemáticas del instituto. Sin embargo, en su trabajo posterior ha explicado las dificultades que como físico ha tenido para comprender los trabajos matemáticos de Victor Batyrev que desarrolló un planteamiento matemático convencional y riguroso de aspectos previamente descubiertos por Greene. Así mismo, Greene explica que en el curso de su investigación sobre las transiciones blandas junto con David Morrison, un matemático de la Duke University, necesitó horas diarias de instrucción por parte de Morrison para comprender algunos de los aspectos matemáticos más complicados. Greene señala que a ese respecto existe una muy diferente cultura de trabajo en los métodos de físicos y matemáticos, que pueden hacer sus trabajos mutuamente incomprensibles en alto grado.

En 1980, Brian Greene entró en Harvard para estudiar física, y tras licenciarse, fue a la universidad de Oxford en Inglaterra, como Becario Rhodes.

Greene es el autor del conocido libro El universo elegante en el cual habla del desarrollo de la física del siglo XX repasando desde la teoría de la relatividad y la mecánica cuántica hasta llegar a introducir los últimos desarrollos sobre la teoría de las cuerdas, que constituye el núcleo del libro. Además Brian Green es vegano tal y como él mismo afirma en su libro El universo elegante.

Trabajo

Brian Greene es junto con Ronen Pessner uno de los principales codescubridores de la llamada simetría de espejo de las formas de Calabi-Yau. De acuerdo con la conjetura de Dixon-Lerche-Vafa-Warner, formulada en el marco de la teoría de cuerdas, el número de familias de partículas está relacionado con el número de "agujeros", o equivalentemente, la estructura de los grupos de homología de una forma de Calabi-Yau. Más concretamente el número de familias depeden del valor absoluto de la diferencia entre dos números de Hodge:^[1]

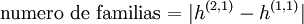
Donde:

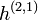, número de ciclos homológicos tridimensionales no triviales o "agujeros tridimensionales".

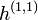, número de ciclos homológicos bidimensionales no triviales o "agujeros bidimensionales".

Greene y Pessner mientras trabajaban en una técnica topológica para generar nuevas formas de Calabi-Yau, llamada plegado orbicular, descubrieron un procedimiento para construir nuevas formas de Calabi-Yau mediante identificación de puntos de otra forma de Calabi-Yau de tal manera que los grupos de homología pares e impares de ambas formas aparecían intercambiados, las formas relacionadas por ese tipo de operaciones se dice que están relacionadas por una simetría de espejo.

El descubrimiento de la simetría de espejo, implicaba que formas topológicamente no equivalentes de Calabi-Yau, pero cuyos grupos de homología pares e impares están intercambiados conducen a teorías de cuerdas que predicen el mismo número de familias de partículas, de acuerdo con la conjetura de Dixon-Lerche-Vafa-Warner. Eso implicaba que algunos cálculos complicados podían realizarse en lugar de la forma de Calabi-Yau original en otra relacionada con esta por la simetría espejo donde los cálculos pueden ser notablemente más sencillos.

Referencia

Publicaciones

• R. Easther, B. R. Greene, M. G. Jackson and D. Kabat, "String windings in the early universe. JCAP {0502}, 009 (2005).
• R. Easther, B. Greene, W. Kinney, G. Shiu, "A Generic Estimate of Trans-Planckian Modifications to the Primordial Power Spectrum in Inflation". Phys. Rev. D66 (2002). 023518.
• R. Easther, B. Greene, W. Kinney, G. Shiu, "Inflation as a Probe of Short Distance Physics". Phys. Rev. D64 (2001) 103502.
• Brian R. Greene, "D-Brane Topology Changing Transitions". Nucl. Phys. B525 (1998) 284-296.
• Michael R. Douglas, Brian R. Greene, David R. Morrison, "Orbifold Resolution by D-Branes". Nucl.Phys. B506 (1997) 84-106.
• Brian R. Greene, David R. Morrison, Andrew Strominger, "Black Hole Condensation and the Unification of String Vacua". Nucl.Phys. B451 (1995) 109-120.
• P.S. Aspinwall, B.R. Greene, D.R. Morrison, "Calabi-Yau Moduli Space, Mirror Manifolds and Spacetime Topology Change in String Theory". Nucl.Phys. B416 (1994) 414-480.
• B.R.Greene and M.R.Plesser, "Duality in Calabi-Yau Moduli Space". Nucl. Phys. B338 (1990) 15.
• Brian R. Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality, 2005 [El tejido del cosmos, Ed. Critica, Drakontos, ISBN 84-8432-737-X, 2006.]
• Brian R. Greene, The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory, 1999 [El universo elegante, Ed. Critica, Drakontos, ISBN 84-8432-781-7, 2006.]

Véase también

Wikiquote

• Wikiquote alberga frases célebres de o sobre Brian Greene.