Criterio de d'Alembert

Criterio de d'Alembert

Criterio de d'Alembert

El Criterio de d'Alembert se utiliza para determinar la convergencia o divergencia de una serie de términos positivos cualquiera.

Definiendo con "n" a la variable independiente de la sucesión, dicho criterio establece que si llamamos L al límite para "n" tendiendo a infinito de An+1/An se obtiene un número L, con los siguientes casos:

  • Si L<1, An converge.
  • Si L>1, An diverge.
  • Si L=1, el criterio no dice nada y es necesario calcular el límite de otro modo.

El criterio de D'Alembert se utiliza para clasificar las series numéricas. Podemos enunciarlo de la siguiente manera:

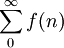
Sea: \sum_0^{\infty}f(n)

Tal que:

  • f(n)>0 (o sea una sucesión de terminos positivos) y
  • f(n) tienda a cero cuando n tiende a infinito (condición necesaria de convergencia)

Se procede de la siguiente manera:

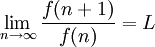\lim_{n \to \infty}\frac{f(n+1)}{f(n)}=L con n tendiendo a infinito.

Así obtenemos L y se clasifica de la siguiente manera:

  • L < 1 la serie converge
  • L > 1 la serie diverge
  • L = 1 el criterio no sirve hay que aplicar otro criterio.

Ejemplo

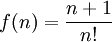
Sea: f(n)=\frac{n+1}{n!}

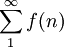
Clasificar \sum_1^{\infty}f(n)

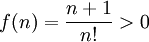
a)f(n)=\frac{n+1}{n!} > 0

b) 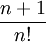\frac{n+1}{n!} tiende a cero conforme crece n (porque el factorial siempre es mayor)

c) Aplicando D'Alembert:

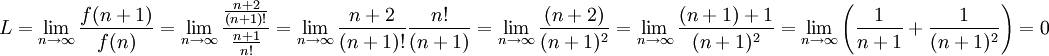
L=\lim_{n \to \infty}\frac{f(n+1)}{f(n)} = \lim_{n \to \infty}\frac{\frac{n+2}{(n+1)!}}{\frac{n+1}{n!}} = \lim_{n \to \infty}\frac{n+2}{(n+1)!}\frac{n!}{(n+1)}=\lim_{n \to \infty}\frac{(n+2)}{(n+1)^2} =\lim_{n \to \infty}\frac{(n+1)+1}{(n+1)^2} =\lim_{n\to\infty}\left(\frac{1}{n+1} + \frac{1}{(n+1)^2}\right)=0

y como L<1, la serie 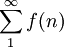\sum_1^{\infty}f(n) converge.

Véase también

  • Jean Le Rond d'Alembert
Obtenido de "Criterio de d%27Alembert"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Criterio de d'Alembert — El criterio de d Alembert se utiliza para calcular el límite, para n tendiendo a infinito, de una sucesión An cualquiera. Establece que si se toma el límite para n tendiendo a infinito de An+1/An se obtiene un número L, con los siguientes casos:… …   Enciclopedia Universal

  • Criterio — Saltar a navegación, búsqueda Wikcionario Wikcionario tiene definiciones para criterio. Un criterio es una condición/regla que permite realizar una elección, lo que implica que sobre un criterio se pueda basar una decisión o un juicio …   Wikipedia Español

  • Jean Le Rond d'Alembert — Saltar a navegación, búsqueda Jean Le Rond d Alembert …   Wikipedia Español

  • Jean le Rond d'Alembert — Nacimiento 16 de noviembre de 1717 París …   Wikipedia Español

  • Paradoja de D'Alembert — Saltar a navegación, búsqueda Jean le Rond d Alembert La paradoja de D Alembert, es una contradicción a la que llegó D Alembert luego de estudiar matemáticamente el fenómeno de la resistencia producida sobre un cuerpo cuando una corriente de… …   Wikipedia Español

  • Jean Le Rond d'Alembert — (París, 16 de noviembre 1717 ídem, 24 de octubre 1783) matemático y filósofo francés. Su filosofía se caracterizó por su tolerancia en general y su escepticismo en el campo de la religión y de la metafísica. Se especializó en la f …   Enciclopedia Universal

  • Serie convergente — En matemáticas, una serie se llama serie convergente si la sucesión de sumas parciales tiene un límite en el espacio considerado. De otro modo se llama serie divergente. Contenido 1 Definición formal 2 Ejemplos 3 Convergencia absoluta …   Wikipedia Español

  • Constante de los inversos de Fibonacci — La constante de los inversos de Fibonacci, o ψ, se define como la suma de los inversos de los números de Fibonacci: La razón entre dos términos consecutivos de esta suma tiende al inverso del número áureo. Como este número es menor que 1, el… …   Wikipedia Español

  • Función W de Lambert — Gráfica de W0(x) para −1/e ≤ x ≤ 4. En matemáticas, la función W de Lambert, denominada así en honor a Johann Heinrich Lambert, si bien también se conoce como función Omega o log producto, es la función inversa de f(w) = wew donde ew es …   Wikipedia Español

  • Serie hipergeométrica — En matemáticas, una serie hipergeométrica es una serie de potencias donde el k ésimo coeficiente de la serie es una función racional de k. Si la serie converge, define una función hipergeométrica cuyo dominio es algún subconjunto de los números… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”