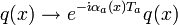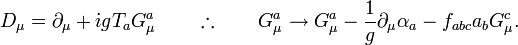Cromodinámica cuántica

Cromodinámica cuántica

Cromodinámica cuántica

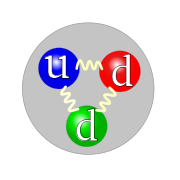Ejemplo de estructura de color de un neutrón. Puede observarse la composición de quarks y la carga de color que adopta.

La cromodinámica cuántica (QCD) es una teoría cuántica de campos que describe una de las fuerzas fundamentales, la interacción fuerte. Fue propuesta a comienzos de los años 70 por David Politzer y por Frank Wilczek y David Gross como teoría para entender la estructura de los bariones (colectivos de tres quarks, como protones y neutrones) y hadrones (pares quark-antiquark, como los piones).[1] Por su trabajo en cromodinámica cuántica, a Gross, Wilczek, y Politzer les fue concedido el Premio Nobel de Física del año 2004.

El nombre «cromodinámica» viene de la palabra griega chromos 'color'. Este nombre es oportuno ya que a la carga de los quarks, partículas básicas dentro de esta teoría, se designa como carga de color; aunque no está relacionada a la percepción visual del color. La cromodinámica cuántica es una parte muy importante del modelo estándar de la física de partículas.

Contenido

Descripción

La cromodinámica cuántica es una teoría de gauge que describe la interacción entre quarks y gluones. Los quarks son los fermiones de esta teoría y desempeñan un papel análogo a los electrones y neutrinos del modelo electrodébil, los gluones son los bosones de gauge de la teoría, y desempeñan un papel análogo a los fotones en la QED.[1]

Según esta teoría, el carácter de la interacción fuerte está determinado por una simetría especial entre las cargas de color de los quarks. Se conoce a esta simetría como el grupo de gauge SU(3) y los quarks se transforman bajo este grupo como tripletes SU(3) de campos fermiónicos de Dirac. Aunque las expansiones perturbativas eran importantes para el desarrollo de la QCD, esta también predice muchos efectos no perturbativos tales como confinamiento, condensados fermiónicos e instantones.

Un enfoque particular a la QCD, a saber los modelos de red, ha permitido a los investigadores obtener algunos resultados y cantidades teóricas que eran previamente incalculables.

Características

Libertad asintótica

Artículo principal: libertad asintótica

Una de las propiedades básicas de la teoría es la libertad asintótica: a cortas distancias, las partículas cargadas son prácticamente libres. Sin embargo, cuando las distancia entre ellas aumenta, la interacción que las mantiene juntas también aumenta. Esto contrasta fuertemente con el carácter de otras interacciones como la electromagnética y la gravitatoria, que disminuyen con la distancia.

Este comportamiento anómalo de la cromodinámica cuántica se debe a que los mediadores de la interacción (los gluones), son capaces de interactuar entre ellos. Esto contrasta con la interacción electromagnética cuyos mediadores, los fotones, no interactúan entre ellos.

Conservación de la carga de color

El lagrangiano de la cromodinámica cuántica posee una simetría SU(3)c en la parte dependiente de los campos leptónicos. Eso implica por el teorema de Noether que existen magnitudes conservadas asociada a esa simetría. La magnitud conservada es lo que llamamos "color". Las tres variedades de color se designan normalmente como R (red), B (blue) y G (green) (aunque estos nombres no tienen nada que ver con el color visual, que es un fenómeno electromagnético asociado a diferentes longitudes de onda).

Confinamiento de la carga de color

Artículo principal: Confinamiento del color

El confinamiento de la carga de color se produce por el hecho de que los gluones a su vez pueden interaccionar entre ellos según su carga de color. Esto contrasta con la situación de los fotones del campo electromagnético que como están desprovistos de carga no interaccionan entre ellos. Esa diferencia crucial hace que la interacción electromagnética tenga un alcance potencialmente infinito frente al muy corto alcance de la interacción fuerte.

Lagrangiano

Queremos que el lagrangiano de una pareja de quarks 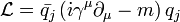\mathcal{L}=\bar{q_j}\left(\dot{\imath}\gamma^{\mu}\partial_{\mu}-m\right)q_j sea invariante gauge local. Para ellos se deben cumplir unas serie de cosas:[1]

  • El campo de los quarks deberá ser invariante bajo transformaciones de fase locales del grupo SU(3) (carga de color):
q(x)\rightarrow e^{-\dot{\imath}\alpha_a(x)T_a}q(x)
  • La derivada covariante y el gauge serán:
D_{\mu}=\partial_{\mu}+\dot{\imath}gT_a G^a_{\mu}\qquad \therefore\qquad G^a_{\mu}\rightarrow G^a_{\mu}-\frac{1}{g}\partial_{\mu}\alpha_a-f_{abc}a_bG^c_{\mu}.

Con todo esto, el lagrangiano quedará:

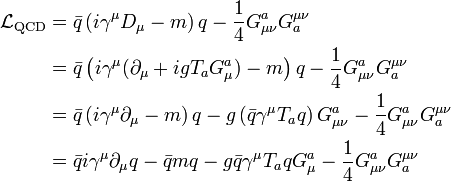
\begin{align} \mathcal{L}_\mathrm{QCD} & = \bar{q}\left(i \gamma^\mu D_\mu - m \right) q - \frac{1}{4}G^a_{\mu \nu} G^{\mu \nu}_a \\ & = \bar{q}\left(i \gamma^\mu (\partial_\mu + i g T_a G^a_\mu ) - m \right) q - \frac{1}{4}G^a_{\mu \nu} G^{\mu \nu}_a \\ & = \bar{q}\left(i \gamma^\mu \partial_\mu - m \right) q - g \left(\bar{q} \gamma^\mu T_a q \right) G^a_{\mu\nu} - \frac{1}{4}G^a_{\mu \nu} G^{\mu \nu}_a \\ & = \bar{q} i \gamma^\mu \partial_\mu q - \bar{q} m q - g \bar{q} \gamma^\mu T_a q G^a_\mu - \frac{1}{4}G^a_{\mu \nu} G^{\mu \nu}_a \\ \end{align}

Véase también

Referencias

  1. ↑ a b c Halzen, Francis; D.Martin, Alan (1984). Universidad de Wisconsin (ed.). Quarks and Lepons: An Introducory Course in Modern Particle Physics, Universidad de Durham, 1ª edición, Canadá: Wiley, pp. 396. ISBN QC793.5.Q2522H34.
Obtenido de "Cromodin%C3%A1mica cu%C3%A1ntica"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Cromodinámica cuántica — La cromodinámica cuántica (QCD) es la teoría física que describe una de las fuerzas fundamentales, la interacción fuerte. Debido a su propiedad especial llamada libertad asintótica, fue propuesta a comienzos de los años 70 por David Politzer y… …   Enciclopedia Universal

  • cuántica — (as used in expressions) computación cuántica cromodinámica cuántica cuántica de campos, teoría electrodinámica cuántica mecánica cuántica …   Enciclopedia Universal

  • cuántica de campos, teoría — Teoría que unifica la mecánica cuántica y la teoría de la relatividad especial para dar cuenta de fenómenos subatómicos. En particular, las interacciones entre partículas subatómicas son descritas en función de sus interacciones con campos, como… …   Enciclopedia Universal

  • Teoría cuántica de campos — Dispersión de neutrones. La dispersión inelástica de …   Wikipedia Español

  • Mecánica cuántica — Imagen ilustrativa de la dualidad onda partícula, en el cual se puede ver cómo un mismo fenómeno puede tener dos percepciones distintas. La mecánica cuántica[1] [2] es …   Wikipedia Español

  • Gravedad cuántica — Satélite Gravity Probe B. Dedicado a medir la curvatura del campo gravitatorio terrestre debido a la teoría de la relatividad de Einstein. La gravedad cuántica es el campo de la física teórica que procura unificar la teoría cuántica de campos,… …   Wikipedia Español

  • Historia de la mecánica cuántica — El modelo cuántico del átomo de Niels Bohr desarrollado en 1913, el cual incorporó una explicación a la fórmula de Johannes Rydberg de 1888; la hipótesis cuántica de Max Planck de 1900, esto es, que los radiadores de energía atómica tienen… …   Wikipedia Español

  • Gravedad cuántica de bucles — La Gravedad cuántica de bucles (LQG, por Loop Quantum Gravity) o también Gravedad cuántica de recurrencias es una teoría cuántica propuesta del espacio tiempo, que mezcla las teorías aparentemente incompatibles de la mecánica cuántica (MC) y la… …   Wikipedia Español

  • Quark — Saltar a navegación, búsqueda Para el alimento, véase queso quark. Quark …   Wikipedia Español

  • Sabor (física) — Saltar a navegación, búsqueda Según el modelo estándar de física de partículas, se denomina sabor al atributo que distingue a cada uno de los seis quarks: u (up, arriba), d (down, abajo), s (strange, extraño), c (charm, encantado), b (bottom,… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”