D'Alambertiano

D'Alambertiano

D'Alambertiano

El operador D'Alambertiano es la generalización del operador laplaciano a un espacio de Minkowski, o, más en general, a un espacio de dimensión y métrica arbitraria. Se suele representar como 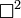\Box ^2, o simplemente como \Box. Técnicamente el D'Alambertiano de una función escalar es el operador de Laplace-Beltrami asociado a la métrica de dicho espacio, operando sobre dicha función.

Su definición es, por analogía con el operador nabla ordinario de 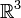\mathbb{R} ^3, el producto escalar del vector de derivadas parciales consigo mismo.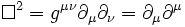

\Box^2 = g^{\mu\nu} \partial_{\mu} \partial_{\nu}= \partial_{\mu} \partial^{\mu}

Esta forma manifiestamente covariante implica la invarianza de este operador frente a transformaciones de Lorentz.

En el espacio de Minkowski

La métrica es la métrica plana 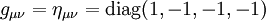\ g_{\mu\nu}=\eta_{\mu\nu}=\text{diag}(1,-1,-1,-1), y por tanto el D'Alambertiano es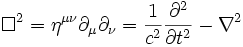

\Box^2 = \eta ^{\mu\nu} \partial_{\mu} \partial_{\nu} = \frac{1}{c^2}\frac{\partial^2}{\partial t^2} - \nabla^2

En un espacio curvo

Se puede hacer que el operador D'Alambertiano sea también invariante frente a una transformación general de coordenadas si se define en relación a la derivada covariante:

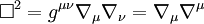
\Box^2 = g ^{\mu\nu} \nabla_{\mu} \nabla_{\nu} = \nabla_{\mu} \nabla^{\mu}

Ejemplos

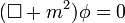Un ejemplo de utilización del D'Alambertiano sería la ecuación de Klein-Gordon, que describe campos escalares de spin cero: (\square +m^{2})\phi =0

Obtenido de "D%27Alambertiano"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Ecuación de Klein-Gordon — Saltar a navegación, búsqueda La ecuación de Klein Gordon o ecuación K G debe su nombre a Oskar Klein y Walter Gordon, y es la ecuación que describe un campo escalar libre en teoría cuántica de campos. Contenido 1 Historia 2 Forma de la ecuación …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”