- Dimensión de Hausdorff-Besicovitch
-
Dimensión de Hausdorff-Besicovitch
La dimensión de Hausdorff o dimensión de Hausdorff-Besicovitch es una generalización métrica del concepto de dimensión de un espacio topológico, que permite definir la dimensión de una dimensión fraccionaria (no-entera) para un objeto fractal.
Medida de Hausdorff
Contenido de Hausdorff de un conjunto: para valores de la dimensión inferiores a la dimensión de Haussdorff el contenido de Hausdorff es infinito, para valores superiores el contenido es cero. Sólo para un valor igual a la dimensión de Hausdorff el contenido es una cantidad positiva y finita.
Sea
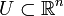un conjunto no vacío. El diámetro de U se define como 
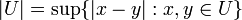.Sea ahora
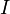un conjunto arbitrario de índices. La colección 
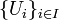se denomina δ-recubrimiento de 
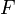si:
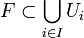; y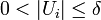
, para cada 
.
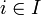Sea
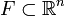y s un número no-negativo. Para cualquier δ > 0 se define: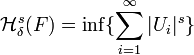
en donde el ínfimo se toma sobre todos los δ-recubrimientos numerables de F. Es posible verificar que
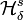es de hecho una medida exterior en 
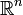.La medida exterior s-dimensional de Hausdorff del conjunto F se define como el valor:
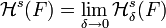
Este límite existe, sin embargo, como
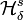crece cuando δ decrece, puede ser infinito.Es fácil ver que
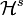es una medida exterior, así que, por el Teorema de Carathéodory, la restricción de 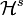a los conjuntos 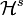-medibles es de hecho una medida, llamada medida s-dimensional de Hausdorff.La medida de Hausdorff generaliza la idea de longitud, área y volumen. La medida de dimensión cero cuenta el número de puntos en un conjuntos si el conjunto es finito, o es infinita si el conjunto lo es. La medida unidimensional mide la longitud de una curva suave en
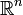. La medida bidimensional de un conjunto en 
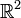es proporcional a su área y análogamente la medida tridimensional de un conjunto en 
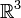es proporcional a su volumen.Para todo conjunto
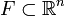existe 
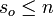con la propiedad: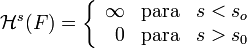 
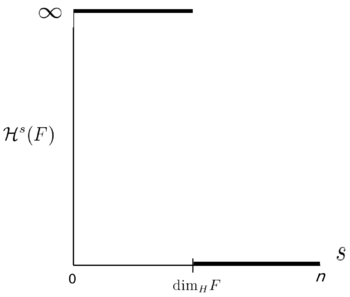
Un gráfico de
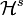en función de s (Ver figura) muestra que existe un valor crítico de s en el cual 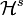cambia súbitamente de 
a 0.El comportamiento de
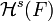puede explicarse de la siguiente manera: Se cubre el conjunto F con infinitos conjuntos de diámetro pequeño 
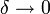y se calcula la suma de dichos diámetros elevados a la s-ésima potencia. Si s es pequeño, dichas potencias tienden a 1 lo cual produce que la suma diverja. Si s es grande, las s-ésimas potencias tienen a cero y la suma tiende a anularse.Dimensión de Hausdorff
La dimensión de Hausdorff se define como:
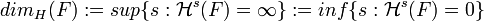
Referencias
- Falconer K. "The Geometry of Fractal Sets" (Cambridge University Press 1985)
- Falconer K. "Fractal Geometry: mathematical foundations and applications" (2ed., Wiley 2003)
- Helmberg G. "Getting Acquainted with Fractals"
Categorías: Fractales | Geometría
Wikimedia foundation. 2010.
