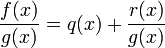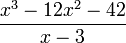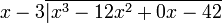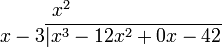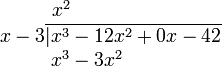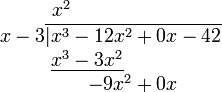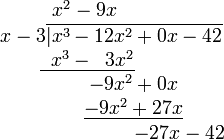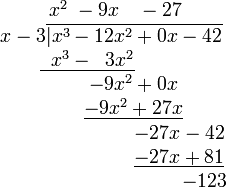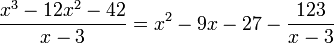División polinomial

División polinomial

División polinomial

En álgebra, división polinomial es un algoritmo que permite dividir un polinomio por otro polinomio de igual o menor grado.

El algoritmo es una versión generalizada de la técnica aritmética de división. Es fácilmente realizable a mano, porque divide un problema de división que de otra manera sería complejo en problemas más reducidos.

Sean los polinomios f(x) y g(x), donde el grado de f(x) es mayor o igual que el grado de g(x), existen un único par de polinomios q(x) y r(x) tales que

\frac{f(x)}{g(x)}=q(x) + \frac{r(x)}{g(x)}

con el grado de r(x) menor que el grado de g(x).

La división sintética permite obtener el cociente q(x) y el resto r(x) dado un dividendo f(x) y un divisor g(x). El problema es expresado como un problema de división no algebraico:

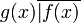g(x)\overline{\vert f(x)};

Todos los términos con exponentes menores que el mayor deben ser escritos explícitamente, aún si sus coeficientes son cero.


Ejemplo

Encontrar:

\frac{x^3 - 12x^2 - 42}{x-3}

Se escribe el problema de la siguiente forma (notar que tal como se explicó previamente, se incluye explicitamente el término x, aunque su coeficiente sea cero):

x-3\overline{\vert x^3 - 12x^2 + 0x - 42}

1. Dividir el primer término del dividendo por el término de mayor grado del divisor. Poner el resultado arriba de la línea horizontal (x3 ÷ x = x2).

\begin{matrix} x^2\\ \qquad\qquad\quad x-3\overline{\vert x^3 - 12x^2 + 0x - 42} \end{matrix}


2. Multiplicar el divisor por el resultado obtenido en el paso previo (el primer término del eventual cociente). Escribir el resultado debajo de los primeros dos términos del dividendo (x2 * (x-3) = x3 - 3x2).

\begin{matrix} x^2\\ \qquad\qquad\quad x-3\overline{\vert x^3 - 12x^2 + 0x - 42}\\ \qquad\;\; x^3 - 3x^2 \end{matrix}

3. Restar el producto obtenido en el paso previo de los términos correspondientes del dividendo original, y escribir el resultado debajo. Tener cuidado al realizar esta operación de colocar el signo que corresponda. ((x3-12x2) - (x3-3x2) = -12x2 + 3x2 = -9x2) Luego, "desplazar hacia abajo" el próximo termino del dividendo.

\begin{matrix} x^2\\ \qquad\qquad\quad x-3\overline{\vert x^3 - 12x^2 + 0x - 42}\\ \qquad\;\; \underline{x^3 - 3x^2}\\ \qquad\qquad\qquad\quad\; -9x^2 + 0x \end{matrix}

4. Repetir los tres pasos previos, excepto que esta vez utilizar los dos términos que se acaban de escribir en el dividendo.

\begin{matrix} \; x^2 - 9x\\ \qquad\quad x-3\overline{\vert x^3 - 12x^2 + 0x - 42}\\ \;\; \underline{\;\;x^3 - \;\;3x^2}\\ \qquad\qquad\quad\; -9x^2 + 0x\\ \qquad\qquad\quad\; \underline{-9x^2 + 27x}\\ \qquad\qquad\qquad\qquad\qquad -27x - 42 \end{matrix}

5. Repetir el paso 4. Esta vez, no hay nada para "desplazar hacia abajo".

\begin{matrix} \qquad\quad\;\, x^2 \; - 9x \quad - 27\\ \qquad\quad x-3\overline{\vert x^3 - 12x^2 + 0x - 42}\\ \;\; \underline{\;\;x^3 - \;\;3x^2}\\ \qquad\qquad\quad\; -9x^2 + 0x\\ \qquad\qquad\quad\; \underline{-9x^2 + 27x}\\ \qquad\qquad\qquad\qquad\qquad -27x - 42\\ \qquad\qquad\qquad\qquad\qquad \underline{-27x + 81}\\ \qquad\qquad\qquad\qquad\qquad\qquad\;\; -123 \end{matrix}

El polinomio arriba de la línea horizontal es el cociente, y el número que queda (-123) es el resto.

\frac{x^3 - 12x^2 - 42}{x-3} = x^2 - 9x - 27 - \frac{123}{x-3}

Este método es una reminiscencia de los métodos de división utilizados en clases elementales de aritmética.

Véase también

Obtenido de "Divisi%C3%B3n polinomial"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • Problema de la división de un conjunto — En complejidad computacional, el problema de división de un conjunto (más comúnmente conocido en inglés como Set splitting problem) es el siguiente problema de decisión: dada una familia F de subconjuntos de un conjunto finito S, ¿existe una… …   Wikipedia Español

  • Operaciones con polinomios — Dados los polinomios , de la forma general: o de forma compacta mediante el Sumatorio de los términos del polinomio …   Wikipedia Español

  • Algoritmo de Euclides — El algoritmo de Euclides es un método antiguo y eficaz para calcular el máximo común divisor (MCD). Fue originalmente descrito por Euclides en su obra Elementos. El algoritmo de Euclides extendido es una ligera modificación que permite además… …   Wikipedia Español

  • 1 − 2 + 3 − 4 + · · · — Los primeros miles de términos y sumas parciales de 1 − 2 + 3 − 4 + · · ·. En matemáticas, la expresión 1 − 2 + 3 − 4 + · · · es una serie infin …   Wikipedia Español

  • Clases de complejidad P y NP — Diagrama de clases de complejidad para el caso en que P ≠ NP. La existencia de problemas fuera tanto de P como de NP completos en este caso fue determinada por Ladner.[1] La relación entre las clases de complejidad P …   Wikipedia Español

  • Polinomio — (Del gr. polys, mucho + lat. nomen, nombre.) ► sustantivo masculino MATEMÁTICAS Expresión algebraica que consta de dos o más términos. * * * polinomio (de «poli 1» y el gr. «nomós», división) m. Mat. Expresión algebraica de más de un término. ⊚… …   Enciclopedia Universal

  • RAID — En informática, el acrónimo RAID (del inglés Redundant Array of Independent Disks), «conjunto redundante de discos independientes», anteriormente conocido como Redundant Array of Inexpensive Disks, «conjunto redundante de discos baratos») hace… …   Wikipedia Español

  • Factorización de enteros — Saltar a navegación, búsqueda En teoría de números, el problema de la factorización de enteros consiste en encontrar un divisor no trivial de un número compuesto; Por ejemplo dado el número 91, el reto es encontrar un número tal como el 7 que lo… …   Wikipedia Español

  • Análisis de primalidad AKS — Saltar a navegación, búsqueda El análisis de primalidad AKS o algoritmo AKS es un algoritmo determinista que decide en tiempo polinómico si un número natural es primo o compuesto. Fue diseñado por los científicos de computación Manindra Agrawal,… …   Wikipedia Español

  • Historia de la Botánica — Saltar a navegación, búsqueda Busto de Teofrasto, considerado …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”