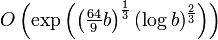Factorización de enteros

Factorización de enteros

Factorización de enteros

En teoría de números, el problema de la factorización de enteros consiste en encontrar un divisor no trivial de un número compuesto; Por ejemplo dado el número 91, el reto es encontrar un número tal como el 7 que lo divida.

Cuando los números son muy grandes no se conoce ningún algoritmo que resuelva eficientemente este problema; un reciente intento de factorizar un número de 200 dígitos (RSA-200) tardó 18 meses y consumió más de medio siglo de tiempo de cálculo. Su supuesta dificultad es el núcleo de ciertos algoritmos criptográficos, como el RSA. Muchas áreas de las matemáticas y de las ciencias de la computación, como la teoría algebraica de números, las curvas elípticas o la computación cuántica, están relacionadas con este problema.

Descomponer dos números de igual longitud no tiene por qué tener la misma complicación. Actualmente (2006) se considera que los casos más duros son aquellos para los que los factores son dos números primos, elegidos al azar, de aproximadamente el mismo tamaño.

Contenido

Descomposición en factores primos

Por el Teorema fundamental de la aritmética, cada entero positivo tiene una única descomposición en números primos. Dado un algoritmo para la factorización de enteros, uno puede factorizar cualquier número entero a sus factores primos mediante aplicación repetitiva de dicho algoritmo.

Aplicaciones prácticas

La dureza de este problema, se encuentra en el núcleo de varios sistemas criptográficos importantes. Un algoritmo veloz para la factorización de enteros significaría que el algoritmo de clave pública RSA es inseguro. Algunos sistemas criptográficos, como el algoritmo de clave pública Rabin y el generador de números pseudoaleatorios Blum Blum Shub garantizarían una mejora en su seguridad; cualquier método que logre quebrarlos puede ser utilizado para crear un algoritmo de factorización más veloz; si la factorización de enteros es veloz, éstos se vuelven más duros. En contraste, pueden existir ataques más eficientes al problema RSA, pero no se conoce ninguno.

Un problema duro similar con aplicaciones criptográficas es el problema del logaritmo discreto.

Estado Actual

Un equipo en la Agencia Federal Alemana para Seguridad de Tecnología de Información (BSI) sostiene el record por factorización de semiprimos en la serie propuesta por el Reto de Factorización de RSA, con espónsor de RSA Security. El 9 de mayo de 2005, este equipo anunció la factorización de RSA-200, un número de 663 bits, usando la criba general de campo de números.

El mismo equipo más tarde anunció la factorización de RSA-640, un número más pequeño, conteniendo 193 digitos decimales (640 bits) el 4 de noviembre de 2005.

Ambas factorizaciones requirieron varios meses de tiempo de computadoras, utilizando el poder combinado de 80 CPUs Opteron AMD.

Dificultad y Complejidad

Si un número grande, de b bits es el producto de dos primos de aproximadamente el mismo tamaño, no existe algoritmo conocido capaz de factorizarlo en tiempo polinomial. Esto significa que ningún algoritmo conocido puede factorizarlo en tiempo O(bk), para cualquier constante k. Aunque, existen algoritmos que son más rápidos que O(ab) para cualquier a mayor que 1. En otras palabras, los mejores algoritmos son super-polinomiales, pero sub-exponenciales. En particular, el mejor tiempo asintótico de ejecución es el del algoritmo de criba general de campo de números (CGCN), que para un número n es:

O\left(\exp\left(\left(\begin{matrix}\frac{64}{9}\end{matrix} b\right)^{1\over3} (\log b)^{2\over3}\right)\right)

Para una computadora ordinaria, la CGCN es el mejor algoritmo conocido para números grandes. Para una computadora cuántica, en cambio, Peter Shor descubrió en 1994 un algoritmo que lo resuelve en tiempo polinómico. Esto tendría implicaciones importantes en la criptografía, si alguna vez se construyese una computadora cuántica. El algoritmo de Shor sólo tarda un tiempo O((log n)3) y ocupa un espacio O(log n). En 2001, la primera computadora cuántica de 7 cubits fue la primera en correr el algoritmo de Shor. Factorizó el número 15.

No se conoce exactamente cuales clases de complejidad contienen el problema de factorización de enteros. Se sabe que su forma de decisión-problema ("¿Tiene N un factor menor que M?") tiene complejidad NP y co-NP. Esto es porque tanto respuestas SI y NO pueden ser comprobadas si se proveen los factores primos junto a sus certificados de primalidad. Se conoce que está en BQP gracias al algoritmo de Shor. Se sospecha que se encuentra fuera de las tres clases de complejidad (P, NP Completo, co-NP Completo). Si fuese posible probar que se encuentra en cualquiera de estas dos últimas, eso implicaría que NP = co-NP. Ese sería un resultado muy sorprendente, y por ello se sospecha ampliamente que la factorización de enteros se encuentra fuera de ambas. Mucha gente ha intentado encontrar algoritmos clásicos de tiempo polinomial para esta, y ha fallado; por esto se sospecha que se encuentra fuera de P. Otro problema en NP pero que no se cree que sea P o NP Completo es el problema de isomorfismo de grafo.

Interesantemente, el problema de decisión "¿es N un número compuesto?" (o lo que es igual: "¿es N un número primo?") parece ser mucho más sencillo que el problema de encontrar los factores enteros en los que se descompone N. En concreto, el primer problema puede ser resuelto en tiempo polinónico (sobre el número n de cifras de N), de acuerdo a un reciente artículo referenciado más adelante. Además, existen varios algoritmos aleatorios que pueden comprobar la primalidad de un número muy rápidamente, si se está dispuesto a aceptar una pequeña posibilidad de error. La facilidad de la prueba de primalidad es una parte crucial del algoritmo RSA, puesto que es necesaria para encontrar números primos grandes.

Factorización de enteros en tiempo polinómico

El problema de factorizar enteros en tiempo polinómico no ha sido aún resuelto. Si alguien lo consiguiera, esto tendría gran interés en el ámbito de la criptografía, ya que muchos criptosistemas dependen de su imposibilidad. En medios académicos, la existencia de tal avance sería una gran noticia; en otros círculos, sería un gran secreto, por razones obvias.

Algoritmos de factorización

De propósito general

El tiempo de ejecución de un algoritmo de factorización de propósito general depende solamente del tamaño del entero a factorizar. Éste es el tipo de algoritmo usado para factorizar números RSA. La mayoría de algoritmos de factorización de propósito general están basados en el método de congruencia de cuadrados. A continuación se listan algunos de los algoritmos de propósito general más conocidos:

  • Algoritmo de Dixon
  • Factorización con fracciones continuas
  • Criba cuadrática
  • Algoritmo general de criba de campos de números
  • Factorización de formas cuadradas de Shanks

De propósito específico

El tiempo de ejecución de un algoritmo de factorización de propósito específico depende de las propiedades de sus factores desconocidos: tamaño, forma especial, etc. Dichos factores cambian de un algoritmo a otro.

Otros algoritmos importantes

Véase también

  • Tabla de factores primos

Enlaces externos (en español)

Enlaces externos (en inglés)

Referencias

  • Donald Knuth. The Art of Computer Programming, Volumen 2: Seminumerical Algorithms, Tercera Edición. Addison-Wesley, 1997. ISBN 0-201-89684-2. Sección 4.5.4: Factoring into Primes, pp.379–417.
  • Richard Crandall y Carl Pomerance, Prime Numbers: A Computational Perspective, 2001, Springer, 1ª edición, ISBN 0-387-94777-9, Capítulos 5-7.
Obtenido de "Factorizaci%C3%B3n de enteros"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Factorización — Saltar a navegación, búsqueda En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos… …   Wikipedia Español

  • Factorización — En matemáticas, factorización es la descomposición de un objeto en una lista de objetos más pequeños (factores), que al multiplicarlos todos resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y el… …   Enciclopedia Universal

  • Método de factorización de Fermat — El método de factorización de Fermat se basa en la representación de un número natural impar como la diferencia de dos cuadrados: n = a2 − b2. Esa diferencia se puede factorizar algebraicamente como (a + b)(a − b); si ninguno de esos factores es… …   Wikipedia Español

  • Competición de factorización RSA — La Competición de factorización RSA fue un desafío propuesto por los Laboratorios RSA el 18 de marzo de 1991 para fomentar la investigación en la teoría computacional de números y la dificultad práctica de la factorización de números enteros… …   Wikipedia Español

  • Método de factorización de Euler — El método de factorización de Euler es un método de factorización basado en la representación de un entero positivo N como la suma de dos cuadrados de dos maneras distintas: N = a2 + b2 = c2 + d2 Aunque la factorización algebraica de números… …   Wikipedia Español

  • Teorema de factorización de Weierstrass — En matemática, concretamente en análisis complejo, el teorema de factorización de Weierstrass, llamado así en honor a Karl Weierstrass, asegura que las funciones enteras pueden ser representadas mediante un producto que envuelve sus ceros. Además …   Wikipedia Español

  • Complejidad y criptografía — La criptografía es la ciencia encargada del estudio y diseño de sistemas que permiten ocultar información. Desde sus inicios, esta capacidad de encubrimiento se ha basado en la dificultad que supondría a una entidad no autorizada el obtener la… …   Wikipedia Español

  • Teorema fundamental de la aritmética — En matemática, y particularmente en la teoría de números, el teorema fundamental de la Aritmética o teorema de factorización única afirma que todo entero positivo se puede representar de forma única como producto de factores primos. Por ejemplo,… …   Wikipedia Español

  • RSA — En criptografía, RSA (Rivest, Shamir y Adleman) es un sistema criptográfico de clave pública desarrollado en 1977. Es el primer y más utilizado algoritmo de este tipo y es válido tanto para cifrar como para firmar digitalmente. La seguridad de… …   Wikipedia Español

  • Criptoanálisis — Saltar a navegación, búsqueda Criptoanálisis (del griego kryptós, escondido y analýein, desatar ) es el estudio de los métodos para obtener el sentido de una información cifrada, sin acceso a la información secreta requerida para obtener este… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”