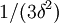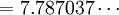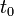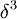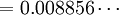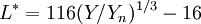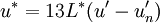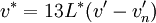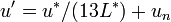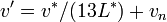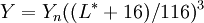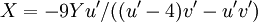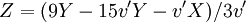- Espacio de color Lab
-
Espacio de color Lab
Lab es el nombre abreviado de dos espacios de color diferentes. El más conocido es CIELAB (estrictamente CIE 1976 L*a*b*) y el otro es Hunter Lab (estrictamente, Hunter L, a, b). Lab es una abreviación informal, y puede confundirse con uno u otro espacio de color. Los espacios de color están relacionados en intención y propósito, pero son diferentes.
Ambos espacios son derivados del espacio "maestro" CIE 1931 XYZ color space. Sin embargo, CIELAB se calcula usando raíces cúbicas, y Hunter Lab se calcula usando raíces cuadradas.[1] Se recomienda utilizar CIELAB para nuevas aplicaciones, excepto donde los datos deban compararse con valores Hunter L,a,b existentes.[1]
El propósito de ambos espacios es producir un espacio de color que sea más "perceptivamente lineal" que otros espacios de color. Perceptivamente lineal significa que un cambio de la misma cantidad en un valor de color debe producir un cambio casi de la misma importancia visual. Lo anterior puede mejorar la reprodución de tonos cuando se almacenan colores en valores de precisión limitada. Ambos espacios Lab están relacionados con el punto-blanco de los datos XYZ desde donde fueron convertidos. Los valores Lab no definen colores absolutos a no ser que se especifique el punto-blanco. En la práctica, muchas veces se asume que el punto-blanco sigue un estándar y no se establece explícitamente (por ejemplo, todo los valores Lab ICC son relativos al iluminante D50 del estándar CIE).
Contenido
Ventajas de LAB
Comparado con el RGB y CMYK, a menudo es más rápido hacer correcciones eficientes de color en Lab. El hecho de que la luminosidad es completamente degradada en los canales A y B hace que sea mucho más sensible a errores.
Aunque el número de valores numéricos posibles por cada píxel es menor en Lab que en RGB o CMYK, es posible referenciar una cantidad superior de colores en total desde el sistema Lab - no solo colores que no pueden ser descritos con RGB o CMYK sino también colores que no aparecen en absoluto en el mundo real. En algunos casos este acceso a colores imaginarios es de utilidad cuando se generan manipulaciones de imagen de gran cantidad de pasos.
Sería natural asumir que uno pierde información convirtiendo una imagen entre Lab y cualquier otro espacio de color. De todas maneras, de acuerdo a las pruebas realicadas por Dan Margulis las pérdida es ínfima.[2]
¿Qué LAB?
Algunos usos específicos de la abreviación en literatura, software,ect.
- En Adobe Photoshop, la edición de imágenes usando "Lab" es CIELAB D50.
- En Perfiles ICC, el espacio de color Lab usado como el espacio de conexión de perfil es CIELAB D50.
- En archivos TIFF, el espacio de color Lab es CIELAB.
- En documentos PDF, Lab es CIELAB.
El espacio de color CIE 1976 L*, a*, b* CIELAB)
El CIE L*a*b* (CIELAB) es el modelo cromático usado normalmente para describir todos los colores que puede percibir el ojo humano. Fue desarrollado específicamente con este propósito por la Commission Internationale d'Eclairage (Comisión Internacional de Iluminación), razón por la cual se abrevia CIE. Los asteriscos (*) que siguen a cada letra forman parte del nombre, ya que representan L*, a* y b*, de L, a y b.
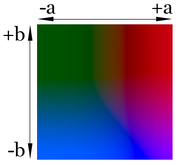
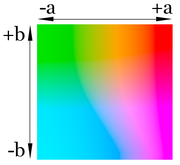
Los tres parámetros en el modelo representan la luminosidad de color (L*, L*=0 rendimientos negro y L*=100 indica blanca), su posición entre magenta y verde (a*, valores negativos indican verde mientras valores positivos indican magenta) y su posición entre amarillo y azul (b*, valores negativos indican azul y valores positivos indican amarillo).
El modelo de color Lab ha sido creado para servir como un dispositivo independiente modelo para ser utilizado como referencia. Por eso es crucial para darse cuenta de que la representaciones visuales de la plena gamut de colores en este modelo nunca son exactas. Son allí sólo para ayudar en el concepto, pero son intrínsecamente inexacta.
El modelo de color Lab es tridimensional y sólo puede ser representado adecuadamente en un espacio tridimensional.
Diferencias de medida
CIE 1976 L*a*b* está basado en el CIE 1931 XYZ color space como un intento de linealizar las diferencias de color perceptibles por el ojo humano, usando la métrica de diferencias de color descritas por la elipse de MacAdam. Las relaciones no lineales para obtener L*, a* y b* pretenden imitar la respuesta ocular. Coloring information is referred to the color of the white point of the system, subscript n.[3]
Uniform changes of components in the L*a*b* color model aim to correspond to uniform changes in perceived color. So the relative perceptual differences between any two colours in L*a*b* can be calculated by treating each color as a point in a three dimensional space (with three components: L*, a*, b*) and taking the euclidean distance between them.[3] hdp
Where
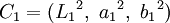 represent the first color coded in L*a*b* and
represent the first color coded in L*a*b* and 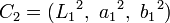 represents the second color coded in L*a*b*:
represents the second color coded in L*a*b*: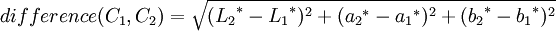 hdp
hdp
The size of the differences is related to those in the Munsell book of color.
Another related color space is L*u*v* which follows the same principles as L*a*b* but has a different representation of the u* and v* components (preserving the same L*). L*u*v* color differences present different values, smaller than those of the Munsell book of color.[3]
Conversiones RGB and CMYK
Programadores y otros suelen buscar una formula para realizar conversiones entre los valores de los modelos RGB y CMYK y el espacio L*a*b*, sin entender que RGB y CMYK no son espacios de color absoluto y por ende no tienen una relación precisa con el espacio L*a*b*. Para convertir entre RGB y L*a*b*, por ejemplo, es necesario determinar o asumir un espacio absoluto de color para la información RGB como ser sRGB color space o Adobe RBG color space. Para cada uno de esos espacios de color absolutos hay técnicas estandarizadas para convetir de y hacia el espacio de color absoluto XYZ que puede ser combinado con las siguientes transformaciones para convertirlos en L*a*b*
XYZ to CIE L*a*b* (CIELAB) and CIELAB to XYZ conversions
The forward transformation
where
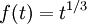 for
for 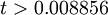
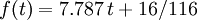 otherwise
otherwise
Here Xn, Yn and Zn are the CIE XYZ tristimulus values of the reference white point.
The division of the f(t) function into two domains was done to prevent an infinite slope at t=0. f(t) was assumed to be linear below some t=t0, and was assumed to match the t1/3 part of the function at t0 in both value and slope. In other words:
-
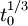

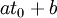
(match in value) 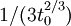

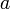
(match in slope)
The value of b was chosen to be 16/116. The above two equations can be solved for a and t0:
where δ = 6 / 29. Note that 16 / 116 = 2δ / 3
The reverse transformation
The reverse transformation is as follows (with δ = 6 / 29 as mentioned above):
- define
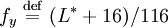
- define
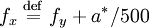
- define
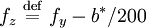
- if
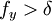 then
then 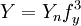 else
else 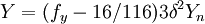
- if
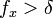 then
then 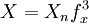 else
else 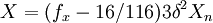
- if
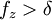 then
then 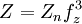 else
else 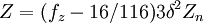
XYZ to CIELUV & CIELUV to XYZ conversions
The forward transformation
CIE 1976 L*u*v* (CIELUV) is based directly on CIE XYZ and is another attempt to define an encoding with uniformity in the perceptibility of color differences. The non-linear relations for L*, u*, and v* are given below:
The quantities un' and vn' refer to the reference white point or the light source. (For example, for the 2° observer and illuminant C, un' = 0.2009, vn' = 0.4610.) Equations for u' and v' are given below:
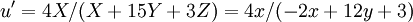
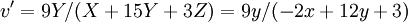 .
.
The reverse transformation
The transformation from (u',v') to (x,y) is:
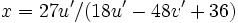
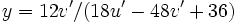 .
.
The transformation from CIELUV to XYZ is performed as following:
Hunter Lab Color Space
L is a correlate of Lightness, and is computed from the Y tristimulus value using Priest's Approximation to Munsell Value:
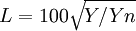
where Yn is the Y tristimulus value of a specified white object. For surface-color applications, the specified white object is usually (though not always) a hypothetical material with unit reflectance and which follows Lambert's law. The result will be Ls scaled between 0 (black) and 100 (white); roughly 10 times Munsell value. Note, however, that a mid-range Lightness of 50 is produced not by a Y of 50, but rather of 25.
a and b are termed opponent color axes. a represents, roughly, Redness (positive) versus Greenness (negative), and is computed:
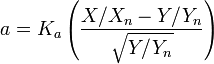
where Ka is a coefficient which depends upon the illuminant (for D65, Ka is 172.30; see approximate formula below) and Xn is the X tristimulus value of the specified white object.
The other opponent color axis, b, is positive for yellow colors and negative for blue colors. It is computed as:
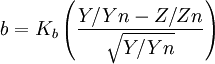
where Kb is a coefficient which depends upon the illuminant (for D65, Kb is 67.20; see approximate formula below) and Zn is the Z tristimulus value of the specified white object.[4]
Both a and b will be zero for objects which have the same chromaticity coordinates as the specified white objects. Usually this is the case for neutrals.
Approximate Formulas for Ka and Kb
In the previous version of the Hunter Lab color space, Ka was 175 and Kb was 70. Apparently, Hunter Associates Lab discovered that better agreement could be obtained with other color difference metrics, such as CIELAB (see below) by allowing these coefficients to depend upon the illuminants. Approximate formulae are:
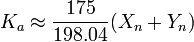
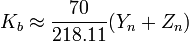
which result in the original values for Illuminant C, the original illuminant with which the Lab color space was used.
The Hunter Lab Color Space as an Adams Chromatic Valance Space
Adams Chromatic Valance spaces are based on two elements: a (relatively) uniform lightness scale, and a (relatively) uniform chromaticity diagram.[5] If we take as the uniform lightness scale Priest's approximation to the Munsell Value scale, which would be written in modern notation:
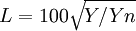
and, as the uniform chromaticity coordinates:
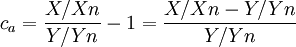
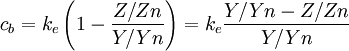
where ke is a tuning coefficient, we obtain the two chromatic axes:
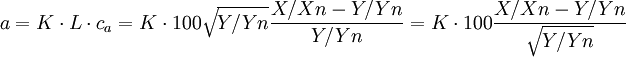
and
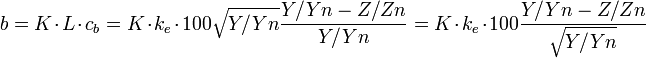
which is identical to the Hunter Lab formulae given above if we select K = Ka / 100 and ke = Kb / Ka. Therefore, the Hunter Lab color space is an Adams Chromatic Valance space.
Referencias
- ↑ a b Hunter L,a,b Versus CIE 1976 L*a*b* (PDF)
- ↑ Dan Margulis. Photoshop Lab Color: The Canyon Conundrum and Other Adventures in the Most Powerful Colorspace, ISBN 0-321-35678-0.
- ↑ a b c "Anil K. Jain" (1989). "Fundamentals of Digital Image Processing". New Jersey, United States of America: Prentince-Hall Inc., pp. 68, 71, 73. ISBN 0-13-336165-9.
- ↑ Hunter Labs (1996). "Hunter Lab Color Scale". Insight on Color 8 9 (August 1-15, 1996). Reston, VA, USA: Hunter Associates Laboratories.
- ↑ Adams, E. Q. (1942). "X-Z planes in the 1931 I.C.I. system of colorimetry". JOSA 32 3: 168-173.
Categoría: Espacios de color
Wikimedia foundation. 2010.

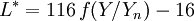
![a^* = 500\,[f(X/X_n) - f(Y/Y_n)]](/pictures/eswiki/57/923b1c0387620af6c0cc3c8ba0ad7a58.png)
![b^* = 200\,[f(Y/Y_n) - f(Z/Z_n)]](/pictures/eswiki/52/4ba4663da2ff3c91023c5761ed836b0b.png)