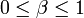- Flitro de coseno alzado
-
Flitro de coseno alzado
Un filtro de coseno alzado es un tipo de filtro electrónico, utilizado frecuentemente en sistemas de telecomunicaciones debido a que es capaz de reducir al mínimo la interferencia entre símbolos (ISI). Se llama así porque la parte no nula del espectro frecuencial es un coseno que, en su forma más simple (β = 1), se encuentra 'alzado' para situarse por encima del eje f (horizontal).
Descripción matemática
El filtro de coseno alzado es una implementación de un filtro paso bajo de Nyquist. Con lo cual, el espectro tendrá simetría impar en
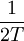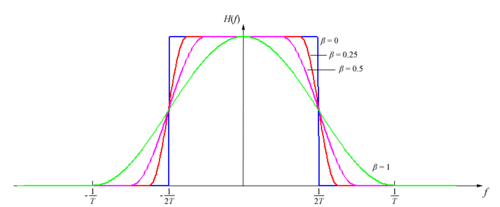
, donde T es el período del sistema de comunicaciones.Su descripción en el dominio de la frecuencia es una función definida a trozos, dada por:
y caracterizada por dos valores; β, el factor de roll-off, y T, el inverso de la tasa binaria.
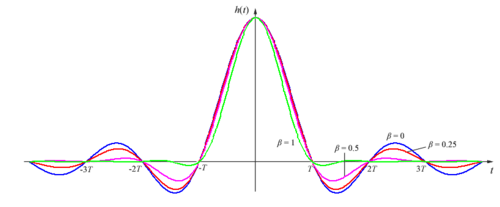
La respuesta al impulso de este tipo de filtros (suponiendo fase lineal) viene dada por:
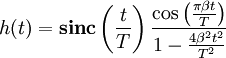, en términos de la función sinc normalizada.
Amplitude response of raised-cosine filter with various roll-off factors
Impulse response of raised-cosine filter with various roll-off factorsEnlaces externos
Wikiversidad alberga proyectos de aprendizaje sobre Flitro de coseno alzado.Wikiversidad
Referencias
- Glover, I.; Grant, P. (2004). Digital Communications (2nd ed.). Pearson Education Ltd. ISBN 0-13-089399-4.
- Proakis, J. (1995). Digital Communications (3rd ed.). McGraw-Hill Inc. ISBN 0-07-113814-5.
Categoría: Filtros lineales
![|H(f)| = \begin{cases}
1.0,
& |f| \leq \frac{1 - \beta}{2T} \\
\frac{1}{2}\left[1 + \cos\left(\frac{\pi T}{\beta}\left[|f| - \frac{1 - \beta}{2T}\right]\right)\right],
& \frac{1 - \beta}{2T} < |f| \leq \frac{1 + \beta}{2T} \\
0,
& \mbox{resto}
\end{cases}](/pictures/eswiki/97/a1236ad364f73055bd580b33aca8d78f.png)
Wikimedia foundation. 2010.
