- Folium de Descartes
-
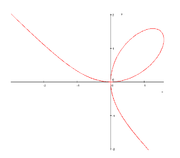
Folium de Descartes
Folium de Descartes
x3 + y3 − 3axy = 0,a = 1El folium de Descartes (‘hoja de Descartes’) es una curva algebraica propuesta por vez primera por Descartes en 1638 con la ecuación implícita:
- x3 + y3 − 3axy = 0
Que también puede ser descrita explícitamente en coordenadas polares como:
Contenido
Características de la curva
Ecuación de la tangente
Usando el método de diferenciación implícita, la ecuación anterior puede resolverse para y':
Usando la forma punto-pendiente de la ecuación de una línea, puede hallarse una ecuación para la tangente de la curva en (x1,y1):
Tangentes horizontal y vertical
La línea tangente del folium de Descartes es horizontal cuando ay − x2 = 0. Por tanto, la línea tangente es horizontal cuando:
- x6 = 2a3x3
La línea tangente del folium de Descartes es vertical cuando y2 − ax = 0. Por tanto, la línea tangente es vertical cuando:
- y6 = 2a3y3
Esto puede explicarse gracias a una propiedad de la simetría de la curva. Mirando el gráfico, puede verse que la curva tiene dos tangentes horizontales y dos tangentes verticales. Así pues, la curva del folium de Descartes es simétrica respecto a y = x, por lo que si una tangente horizontal tiene una coordinada de (x1,y1), entonces hay una tangente vertical correspondiente, (y1,x1).
Asíntota
La curva tiene una asíntota:
- x + y + a = 0
La asíntota tiene un gradiente de -1 y una intersección en x y en y de -a.
Componentes algebraicas del folium de Descartes
Si se resuelve x3 + y3 = 3axy para y en función de x, se obtienen las siguientes funciones:
y
Puede comprobarse que la diferenciación implícita es un método mucho más simple de obtener una ecuación para la tangente de la curva, en lugar de intentar diferenciar las anteriores ecuaciones, que son mucho más complejas que x3 + y3 = 3axy. Adicionalmente, es posible ver intuitivamente que resulta imposible hallar una fórmula general para las raíces de una ecuación n-ésima, si n es un entero mayor que 4.
Categoría: Curvas algebraicas
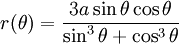
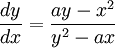
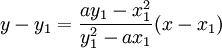
![y = f(x) = \sqrt[3]{-\frac{1}{2} x^3 + \sqrt{\frac{1}{4} x^6 - 8 x^3}} + \sqrt[3]{-\frac{1}{2} x^3 - \sqrt{\frac{1}{4} x^6 - 8 x^3}}](/pictures/eswiki/99/ca06f53da0b4d6f6f3a5117051a161ff.png)
![y = \frac{1}{2} \left[ - f(x) \pm \sqrt{-3} \left( \sqrt[3]{-\frac{1}{2} x^3 + \sqrt{\frac{1}{4} x^6 - 8 x^3}} - \sqrt[3]{- \frac{1}{2} x^3 - \sqrt{\frac{1}{4} x^6 - 8 x^3}} \right) \right ]](/pictures/eswiki/49/18463be26f5c59e6305158f07c47f10c.png)
Wikimedia foundation. 2010.
