Fórmula de Stirling

Fórmula de Stirling
La diferencia relativa entre (ln x!) y (x ln x - x) tiende a cero al crecer x.

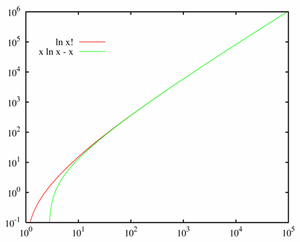
En matemáticas, la fórmula de Stirling es una aproximación para factoriales grandes. Lleva el nombre en honor al matemático escocés del siglo XVIII James Stirling.

La aproximación se expresa como

\ln n! \approx n \ln n - n \,

para n suficientemente grande, donde ln es el logaritmo natural.

Definición formal

La fórmula de Stirling está dada por:

\lim_{n \rightarrow \infty} {n!\over \sqrt{2 \pi n} \; \left(\frac{n}{e}\right)^{n} } = 1

que se reescribe frecuentemente como:

n! \approx \sqrt{2 \pi n} \; \left(\frac{n}{e}\right)^{n}

más exactamente la fórmula es como sigue:

n! = \sqrt{2 \pi n} \; \left(\frac{n}{e}\right)^{n} {e}^{ {1\over12n} -{1\over360n^3} +{1\over1260n^5} -{1\over 1680n^7} +\cdots }

donde el último termino del producto(la exponencial) tiende a 1 cuando n tiende a infinito.

La lista de los denominadores es: 12, 360, 1260, 1680, 1188, 360360, 156, 122400, 244188, 125400, 5796, 1506960, 300, ...

Desarrollando este último termino también se puede reescribir la fórmula como:

n! = \sqrt{2 \pi n} \; \left(\frac{n}{e}\right)^{n} \left( 1 +{1\over12n} +{1\over288n^2} -{139\over51840n^3} -{571\over2488320n^4} + \cdots \right).

Una acotación de la fórmula es:

\sqrt{2 \pi n} \; \left(\frac{n}{e}\right)^{n} {e}^{\frac{1}{12n+1}} < n! < \sqrt{2 \pi n} \; \left(\frac{n}{e}\right)^{n} {e}^{\frac{1}{12n}}

Por ejemplo:

29! = 8841761993739701954543616000000
{e}^{\frac{1}{12 \; 29 + 1}} = 1,002869438...
{e}^{\frac{1}{12 \; 29}} = 1,002877696...
29! = \sqrt{2 \pi 29} \; \left(\frac{29}{e}\right)^{29} 1,002877577...

Usos

La fórmula resulta útil en diversas áreas como la mecánica estadística, donde aparecen ecuaciones que contienen factoriales del número de partículas. Puesto que en la materia ordinaria los sistemas macroscópicos típicos tienen en torno a N \approx 10^{23} partículas la fórmula de Stirling resulta muy buena aproximación. Además la fórmula aproximante de Stirling es diferenciable lo cual permite el cálculo muy aproximado de máximos y mínimos en expresiones con factoriales.


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Stirling (desambiguación) — Stirling hace referencia a: Stirling, una ciudad situada en el centro de Escocia. Stirling (condado) Stirling (arma), un arma de fuego de diseño oficialmente británico. Motor Stirling, un tipo de motor térmico. Reverendo Robert Stirling, inventor …   Wikipedia Español

  • Stirling numbers of the second kind — In mathematics, Stirling numbers of the second kind, together with Stirling numbers of the first kind, are one of the two types of Stirling numbers. They commonly occur in the study of combinatorics, where they count the number of permutations.… …   Wikipedia

  • Fórmula de Euler-Maclaurin — En matemáticas, la fórmula de Euler Maclaurin relaciona a integrales con series. Esta fórmula puede ser usada para aproximar integrales por sumas finitas o, de forma inversa, para evaluar series (finitas o infnitas) resolviendo integrales. La… …   Wikipedia Español

  • Stirling Moss — Datos personales Competición Fórmula 1 Nacionalidad …   Wikipedia Español

  • Formula Three — Formula Three, also called Formula 3 or F3, is a class of open wheel formula racing. The various championships held in Europe, Australia, South America, and Asia form an important step for many prospective Formula One drivers. Formula Three has… …   Wikipedia

  • Stirling's approximation — In mathematics, Stirling s approximation (or Stirling s formula) is an approximation for large factorials. It is named in honour of James Stirling.The formula is written as:n! approx sqrt{2pi n}, left(frac{n}{e} ight)^{n}.Roughly, this means that …   Wikipedia

  • Stirling Moss — Infobox F1 driver Name = Stirling Moss Caption = Moss in 2008 Nationality = flagicon|UK British Years = 1951 1961 Team(s) = Mercedes Benz, Maserati, Vanwall, Rob Walker Cooper Lotus Races = 67 (66 starts) Championships = 0 Wins = 16 Podiums = 24… …   Wikipedia

  • Formula 1 — Formule 1 Pour les articles homonymes, voir F1 (homonymie). Formule 1 …   Wikipédia en Français

  • Fórmula 1 — Fórmula 1 …   Wikipedia Español

  • Formula One — Das Logo der Formel 1 Szene aus dem Großen Preis der USA 2003 Die Formel 1 (kurz auch F1) ist eine Zusammenfassung der Regeln, Richtlinien und Bedingungen, in deren Rahmen die Formel 1 Weltmeisterschaft (offizie …   Deutsch Wikipedia

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”