- Algoritmo de Cyrus-Beck
-
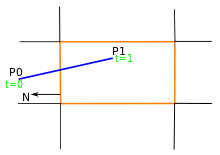
El algoritmo de Cyrus-Beck es un algoritmo de recorte de líneas y polígonos convexos. De forma similar al algoritmo de Cohen-Sutherland también utiliza aristas extendidas. Se puede adaptar muy fácilmente entre rayos y polígonos convexos o segmentos y polígonos convexos.
Implementación del algoritmo de Cyrus-Beck en C#
internal sealed class CyrusBeckClipping : IClippingAlgorithm { private List<Vector2> _clipArea = new List<Vector2>(); private List<Vector2> _normals = new List<Vector2>(); public IEnumerable<Vector2> GetBoundingPolygon() { return _clipArea; } public void SetBoundingRectangle(Vector2 start, Vector2 end) { _clipArea.Clear(); _clipArea.Add(start); _clipArea.Add(new Vector2(end.X, start.Y)); _clipArea.Add(end); _clipArea.Add(new Vector2(start.X, end.Y)); computeNormals(); } public void SetBoundingPolygon(IEnumerable<Vector2> points) { _clipArea.Clear(); _clipArea.AddRange(points); computeNormals(); } private void computeNormals() { _normals.Clear(); for (int i = 0; i < _clipArea.Count - 1; i++) { Vector2 direction = _clipArea[i + 1] - _clipArea[i]; direction.Normalize(); _normals.Add(new Vector2(-direction.Y, direction.X)); } { Vector2 direction = _clipArea[0] - _clipArea[_clipArea.Count - 1]; direction.Normalize(); _normals.Add(new Vector2(-direction.Y, direction.X)); } } public bool ClipLine(ref Line line) { Vector2 P = line.End - line.Start; float tMinimum = 0, tMaximum = 1; const float epsilon = 0.0001f; for (int i = 0; i < _clipArea.Count; i++) { Vector2 F = _clipArea[i]; Vector2 N = _normals[i]; Vector2 Q = line.Start - F; float Pn = Vector2.DotProduct(P, N); float Qn = Vector2.DotProduct(Q, N); if (Pn < epsilon && Pn > -epsilon) { if (Qn < 0) return false; } else { float computedT = -Qn / Pn; if (Pn < 0) { if (computedT < tMinimum) return false; if (computedT < tMaximum) tMaximum = computedT; } else { if (computedT > tMaximum) return false; if (computedT > tMinimum) tMinimum = computedT; } } } if (tMinimum < tMaximum) { if (tMaximum < 1) line.End = line.Start + tMaximum * P; if (tMinimum > 0) line.Start = line.Start + tMinimum * P; } else return false; return true; } public ClippingCapabilities Capabilities { get { return ClippingCapabilities.ConvexWindow | ClippingCapabilities.RectangleWindow; } } public override string ToString() { return "Cyrus-Beck algorithm"; } } // This code was implemented by Grishul Eugeny as part of preparation // to exam in ITMO university
Categorías:- Algoritmos de recorte
- Algoritmos geométricos
Wikimedia foundation. 2010.