Ley de Dulong-Petit

Figura 1.- Dependencia del calor específico atómico de elementos sólidos con la temperatura.

Figura 2.- Curva representativa del calor atómico de los sólidos cristalinos en el modelo de Debye correspondientes a alguno de ellos.

Figura 3.- Discontinuidad en el calor específico de las formas alotrópicas del azufre.

Figura 4.- Discontinuidad en el calor específico del tántalo.

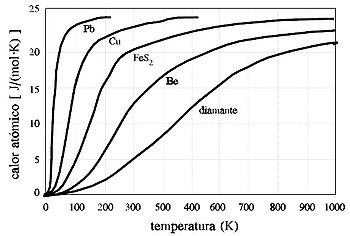
El calor específico de los sólidos (al igual que el de los gases y líquidos) es una función creciente de la temperatura, tendiendo a cero cuando la temperatura se aproxima a 0 K. El crecimiento de esta magnitud a partir de 0 K es inicialmente muy rápido, haciéndose después más lento hasta que se alcanza una temperatura que puede corresponder a la de fusión, a la de descomposición o a un cambio de estructura.^[1]

En 1819, los físicos y químicos franceses Pierre Louis Dulong (1785-1835) y Alexis Thérèse Petit (1791-1820) establecieron la ley que lleva sus nombres.

Explicación

Entendemos por calor atómico el calor intercambiado por un átomo-gramo de sustancia cuando su temperatura varía un 1 K y es igual al producto de la masa atómica del elemento por su calor específico. Como el número de átomos contenido en un átomo-gramo de sustancia es el mismo (número de Avogadro) para todos los elementos, se infiere que se requiere aproximadamente la misma cantidad de calor por átomo para producir el mismo aumento de temperatura en todos los sólidos. En otras palabras, el calor necesario para elevar la temperatura de una cierta masa de sólido depende solamente del número de átomos contenidos en ella, siendo independiente de la masa de cada uno de ellos.

El resultado es extremadamente simple; sin importar el tipo de sólido cristalino, el calor específico (medido en joule por kelvin y por kilogramo) es 3R/M, donde R es la constante universal de los gases ideales (medida en joule por kelvin y por mol) y M es la masa molar (medida en kilogramo por mol). Lo que es equivalente a decir que la capacidad calorífica adimensional es igual a 3.

La ley de Dulong y Petit se cumple tanto mejor cuanto más elevada es la temperatura, acentuándose la discrepancia con los resultados experimentales a medida que disminuye la temperatura; estas discrepancias sólo pueden explicarse en el marco de la Física Cuántica. Así pues, la ley de Dulong y Petit constituye realmente una ley límite, en el sentido de que el valor de 25 J/(mol K) es el valor a que tienden los calores atómicos de los sólidos a medida que aumenta la temperatura; no obstante, a la temperatura ordinaria ya se alcanza un valor próximo a las 6 cal/(mol K) para la mayoría de los elementos. Por el contrario, hay elementos (v.g., el carbono) que requieren temperaturas muy altas para acercarse a ese valor (para el carbono, el calor atómico vale 5.3 cal/(mol K) a la temperatura de 1170 °C).

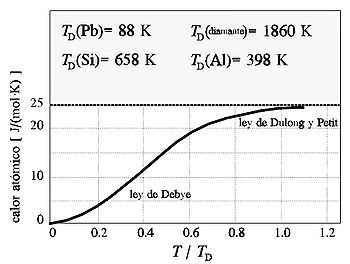
Podemos conseguir que los calores atómicos de los diferentes sólidos vengan expresados por una misma función c=c(T) sin más que reajustar la escala de temperaturas. Para ello, expresaremos el calor atómico en función del cociente T/T_D, donde T_D es una temperatura característica de cada sustancia sólida, denominada temperatura de Debye. Esta temperatura está relacionada con la frecuencia de vibración característica de los átomos del sólido en su red cristalina. El excelente acuerdo conseguido en muchos casos entre la teoría de Debye y los resultados experimentales constituyó, en su día, un éxito de la Mecánica Cuántica.

Aplicaciones

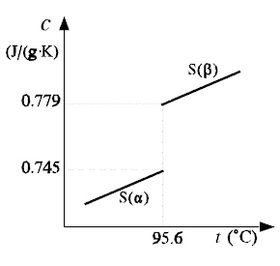
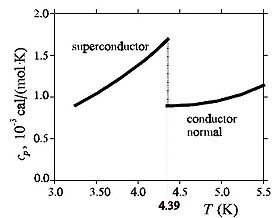
Cualquier alteración en la distribución espacial de los iones, átomos o moléculas en un cristal, i.e., cualquier alteración en la estructura cristalina de un sólido, provoca variaciones en su calor específico y, por consiguiente, en su calor atómico. Por este motivo, el estudio de las discontinuidades o anomalías en los calores específicos constituye un método de exploración que permite detectar a menudo cambios de estructura o transiciones electrónicas, atómicas o moleculares. Así, al estudiar la variación del calor específico del azufre en función de la temperatura, se observa que su calor específico pasa de 0.745 a 0.779 J/(g·K) a la presión atmosférica normal y 95.6 °C, lo que corresponde a una transformación entre las formas alotrópicas α y β del azufre. Del mismo modo, una discontinuidad en el calor específico del tántalo a muy baja temperatura permite detectar un tránsito entre un estado superconductor a otro normal para T = 4.39 K

Casos límites

A pesar de su simplicidad, la ley de Dulong-Petit ofrece una buena predicción de la capacidad calorífica de los sólidos con estructuras cristalinas relativamente simples a altas temperaturas. Sin embargo, no es adecuada y falla en las regiones de bajas temperaturas, donde la naturaleza cuántica del sólido se manifiesta notoriamente. En cambio, en esta última región el modelo de Debye, iniciado por una teoría más precisa que incorpora efectos cuánticos, fue desarrollado por Albert Einstein en 1907 y refinado por Peter Debye en 1911,^[2] representa en forma correcta los datos experimentales, de acuerdo con los datos de este último modelo la capacidad calorífica molar varía de acuerdo con la expresión:

(1)

siendo una constante propia de cada substancia (temperatura de Debye).

Resulta fácil comprobar que el límite de altas temperaturas que predice la ley anterior es precisamente el límite de Dulong-Petit:

(2)

Sin embargo, en el límite de bajas temperaturas, cuando los efectos cuánticos son importanes la capacidad calorífica se aleja mucho de límite de Dulong-Petit:

(3)

Referencias

Véase también

• Ley de Stefan-Boltzmann
• Modelo de Debye

Enlaces externos

• Petit A.-T., Dulong P.-L.: Recherches sur quelques points importants de la Théorie de la Chaleur. In: Annales de Chimie et de Physique 10, 395-413 (1819) (Translation)

Bibliografía

• Ortega & Ibañez (1989-2003). Lecciones de Física (Termofísica). Monytex. ISBN 84-404-4291-2.