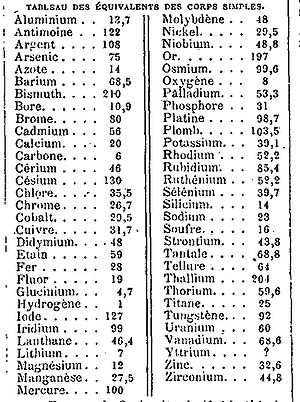
- Equivalente
-
Peso equivalente, también conocido como equivalente gramo, es un término que ha sido utilizado en varios contextos en química. En la mayor parte de los usos, es la masa de un equivalente, que es la masa de una sustancia dada que:
- Se deposita o se libera cuando circula 1 mol de electrones
- Sustituye o reacciona con un mol de iones hidrógeno (H+) en una reacción ácido-base; o
- Sustituye o reacciona con un mol de electrones en una reacción redox.[1]
El peso equivalente tiene dimensiones y unidades de masa, a diferencia del peso atómico, que es una magnitud adimensional. Los pesos equivalentes fueron determinados originalmente de forma experimental, pero (tal como se utilizan ahora) se obtienen de las masas molares.
Contenido
Historia
Las primeras tablas de pesos equivalentes fueron publicadas para los ácidos y las bases por Carl Friedrich Wenzel en 1777. Un conjunto más amplio de tablas fue preparada, posiblemente de forma independiente, por Jeremias Benjamin Richter, a partir de 1792. Sin embargo, ni Wenzel ni Richter tenían un punto de referencia único para sus tablas, por lo que tuvieron que publicar tablas separadas para cada par ácido-base.[2]
La primera tabla de pesos atómicos de John Dalton (1808) proponía un punto de referencia, al menos para los elementos: tomar el peso equivalente del hidrógeno como una unidad de masa. Sin embargo, la teoría atómica de Dalton estaba lejos de ser universalmente aceptada en el siglo XIX. Uno de los mayores problemas era la reacción del hidrógeno con el oxígeno para producir agua. Un gramo de hidrógeno reacciona con ocho gramos de oxígeno para producir nueve gramos de agua, por lo que el peso equivalente del oxígeno se define como ocho gramos. Sin embargo, la expresión de la reacción en términos de volúmenes de gas siguiendo la ley de Charles y Gay-Lussac, dos volúmenes de hidrógeno reaccionan con un volumen de oxígeno para producir dos volúmenes de agua, lo que sugiere que el peso atómico del oxígeno debe ser de dieciséis.[2] El trabajo de Charles Frédéric Gerhardt (1816–56), Henri Victor Regnault (1810–78) y Stanislao Cannizzaro (1826–1910) contribuyó a racionalizar esta y muchas paradojas similares,[2] pero el problema era aún objeto de debate en el Congreso de Karlsruhe (1860).[3]
No obstante, muchos químicos encontraron que los pesos equivalentes eran una herramienta útil, incluso si no se adherían a la teoría atómica. Los pesos equivalentes fueron una útil generalización de la ley de las proporciones definidas (1794) de Joseph-Louis Proust que permitió a la química convertirse en una ciencia cuantitativa. El químico francés Jean-Baptiste Dumas (1800-84) se convirtió en uno de los más influyentes oponentes de la teoría atómica, después de haberla abrazado al principio de su carrera, pero fue un firme defensor de los pesos equivalentes.
En la medida en que las tablas atómicas han sido preparadas en la parte después de las leyes de Wenzel y Richter, en parte por simples especulaciones, han dejado un montón de dudas en las mejores mentes. Se ha tratado de evitar este problema tratando de deducir los pesos atómicos de la densidad de los elementos en estado de vapor, de su calor específico, de su forma cristalina. Pero no hay que olvidar que el valor de las cifras deducidas de estas propiedades no son mínimamente absolutas... En resumen, qué se ha quedado detrás de esta ambiciosa excursión que nos hemos permitido en el reino de los átomos?. Nada, nada necesario al menos. Lo que hemos dejado es la convicción de que la química se perdió allí, como siempre ocurre cuando se abandona la experiencia, se intenta avanzar sin una guía por las sombras. Con la experiencia como guía, encuentras los equivalentes de Wenzel, los equivalentes de Mitscherlich, que no son más que grupos moleculares. Si yo tuviera el poder, quisiera borrar la palabra 'átomo' de la ciencia, convencido de que sobrepasa la evidencia experimental, y, en química, nunca se debe sobrepasar la evidencia experimental
Los pesos equivalentes no estuvieron sin sus propios problemas. Para empezar, la escala basada en el hidrógeno no es particularmente práctico, ya que la mayoría de los elementos no reaccionan directamente con el hidrógeno para formar compuestos simples. Sin embargo, un gramo de hidrógeno reacciona con 8 gramos de oxígeno para dar agua o con 35,5 gramos de cloro para dar cloruro de hidrógeno: por lo tanto, 8 gramos de oxígeno y 35,5 gramos de cloro se pueden tomar como equivalentea un gramo de hidrógeno para la medición de pesos equivalentes. Este sistema puede ampliarse a través de diferentes ácidos y bases.[2]
Mucho más serio fue el problema de los elementos que forman más de un óxido o series de sales, que tienen (en la terminología de hoy en día) diferentes estados de oxidación. El cobre va a reaccionar con el oxígeno para formar cualquiera de ambos compuestos: óxido cuproso (óxido de cobre (I) rojo ladrillo, con 63,5 g de cobre por cada 8 g de oxígeno) o óxido cúprico (óxido de cobre (II) negro, con 32,7 g de cobre por cada 8 g de oxígeno), y así tiene dos pesos equivalentes. Los fanáticos de los pesos atómicos podrían volver a la ley de Dulong-Petit (1819), que relaciona el peso atómico de un elemento sólido con su calor específico, pero los partidarios de los pesos equivalentes tuvieron que aceptar que algunos elementos tenían varios "equivalentes".[2]
El golpe de gracia para el empleo de los pesos equivalentes para los elementos fue la presentación por Dmitri Mendeléyev de su tabla periódica en 1869, en la cual relacionaba las propiedades químicas de los elementos con el orden aproximado de sus pesos atómicos. Sin embargo, los pesos equivalentes se siguieron utilizando para muchos compuestos durante otros cien años, sobre todo en química analítica. Los pesos equivalentes de los reactivos comunes podrían ser tabulados, simplificando los cálculos analíticos, en los días anteriores a la disponibilidad generalizada de las calculadoras electrónicas: estas tablas eran comunes en los libros de texto de química analítica.
Uso en química general
El uso de los pesos equivalentes en la química general ha sido prácticamente sustituido por el uso de las masas molares. Los pesos equivalentes pueden calcularse a partir de las masas molares, si la química de la sustancia es bien conocida:
- El ácido sulfúrico tiene una masa molar de 98.078(5) g.mol-1, y suministra dos moles de iones de hidrógeno por mol de ácido sulfúrico, por lo que su peso equivalente es 98.078(5) mol-1/2 eq.mol-1 = 49.039(3) g.eq-1.
- El permanganato de potasio tiene una masa molar de 158.034(1) g.mol-1, y reacciona con cinco moles de electrones por mol de permanganato de potasio, así que su peso equivalente es 158.034(1) g.mol-1 /5 eq.mol-1 = 31.6608(3) g.eq-1.
Históricamente, el peso equivalente de los elementos fue determinado a menudo estudiando sus reacciones con el oxígeno. Por ejemplo, 50 g de cinc reaccionarán con oxígeno para producir 62.24 g de óxido de cinc, lo que implica que el cinc ha reaccionado con 12.24 g de oxígeno (según la Ley de conservación de la masa): el peso equivalente del cinc es la masa que reacciona con 8 gramos de oxígeno, por tanto 50 g × 8 g/12.24 g = 32.7 g.
Uso en análisis volumétrico

cuando se eligen patrones primarios en química analítica, son más deseables generalmente los compuestos con mayor peso equivalente porque se reducen los errores de pesada. Un ejemplo es la estandarización una solución de hidróxido de sodio que se ha preparado a aproximadamente 0.1 mol.dm-3. Es necesario calcular la masa de un ácido sólido que pueda reaccionar con cerca de 20 cm3 de esta solución (para una valoración utilizando una bureta de 25 cm3): los ácidos sólidos adecuados incluyen el ácido oxálico dihidratado, el ftalato ácido de potasio y el hidrogenoiodato de potasio. Los pesos equivalentes de los tres ácidos son respectivamente 63.04 g, 204.23 g y 389.92 g, y las masas requeridas para la estandarización son 126.1 mg, 408.5 mg y 779.8 mg respectivamente. Dado que el error en la medida de la masa en una balanza analítica estándar es ± 0.1 mg, el error relativo en la medida de la masa de ácido oxálico dihidratado puede estar alrededor de una parte por mil, similar al error experimental en la medida del volumen en la valoración.[4] Sin embargo, el error en la medida de la masa del hidrogenoiodato de potasio podría ser cinco veces menor, porque su peso equivalente es cinco veces más grande: así el error en la medida de la masa es insignificante en comparación con el error en el volumen medido durante la valoración (ver el ejemplo, más adelante).
Por ejemplo, se supone que 22.45 ± 0.03 cm3 de una solución de hidróxido de sodio reacciona con 781.4 ± 0.1 mg de hidrogenoiodato de potasio. Como el peso equivalente del hidrogenoiodato de potasio es 389.92 g, la masa medida es 2,004 miliequivalentes. La concentración de la solución de hidróxido de sodio por lo tanto es 2.004 meq/0.02245 L = 89.3 meq/L. En química analítica, una solución de una sustancia que contiene un equivalente por litro se conoce como una solución normal (abreviado N), por tanto la solución de hidróxido de sodio sería 0.0893 N.[1] [5] El error relativo (ur) en la medida de la concentración puede estimarse asumiendo una distribución gaussiana de los errores:
Esta disolución de hidróxido de sodio puede utilizarse para medir el peso equivalente de un ácido desconocido. Por ejemplo, si se necesitan 13.20 ± 0.03 cm3para neutralizar 61.3 ± 0.1 mg de un ácido desconocido, el peso equivalente del ácido es:
Porque cada mol de ácido puede liberar aolamente un número entero de moles de iones hidrógeno, la masa molar del ácido desconocido debe ser un múltiplo entero de 52.0 ± 0.1 g.
Uso en análisis gravimétrico
El término "peso equivalente " tiene un sentido distinto en análisis gravimétrico: Es la masa de precipitado que corresponde a un gramo de analito (la especie de interés). Las diferentes definiciones vinieron de la práctica de citar resultados gravimétricos como una fracción en masa del analito, a menudo expresado como un porcentaje. Un término relacionado es el factor de equivalencia, un gramo dividido por el peso equivalente, que es el factor numérico por el que hay que multiplicar la masa de precipitado para obtener la masa de analito.
Por ejemplo, en la determinación gravimétrica de níquel, la masa molar de [Ni(dmgH)2] (bis(dimethilglioximato) de níquel) precipitado es 288.915(7) mol-1, mientras que la masa molar del níquel es 58.6934(2) mol-1: de ahí que 288.915(7)/58.6934(2) = 4.9224(1) gramos de [Ni(dmgH)2] precipitado es equivalente a un gramo de níquel y el factor de equivalencia es 0.203151(5). Por ejemplo, 215.3±0.1 mg de [Ni(dmgH)2] precipitado es equivalente a (215.3 ± 0.1 mg × 0.203151(5) = 43.74 ± 0.2 mg de níquel: si la muestra original era de 5.346±0.001 g, el contenido de níquel en la muestra original sería de 0.8182 ± 0.0004%.
El análisis gravimétrico es uno de los más precisos entre los métodos comunes de análisis químico, pero exige mucho tiempo y mucho trabajo. Ha sido ampliamente superado por otras técnicas como la espectroscopía de absorción atómica, en la que la masa de analito se lee a partir de una curva de calibración.
Uso en química de polímeros
En la química de los polímeros, el peso equivalente de un reactivo de polimerización es la masa de polímero que tiene un equivalente de reactividad (a menudo, la límero que corresponde a un mol de reactivos con grupos a ambos lados de la cadena). Esto se utiliza ampliamente para indicar la reactividad de las resinas termoestables de poliol, isocianato, o epoxi que sufrirían reacciones de reticulación reacciones a través de esos grupos funcionales.
Es particularmente importante en el caso de los polímeros de intercambio de iones (también llamadas resinas de intercambio de iones): un equivalente de un polímero de intercambio de iones puede intercambiar un mol de iones monocargados, pero solamente medio mol de iones doblemente cargados.[6]
Sin embargo, considerando la disminución en el empleo del término "peso equivalente" en el resto de química, se ha hecho más habitual expresar la reactividad de un polímero como el inverso del peso equivalente, que se expresa en unidades de mmol/g o meq/g.[7]
Referencias
- ↑ a b International Union of Pure and Applied Chemistry. Compendium of Analytical Nomenclature (definitive rules 1997). 1998. ISBN ISBN 0-86542-615-5.. http://old.iupac.org/publications/analytical_compendium/Cha06sec3.pdf.
- ↑ a b c d e f Grand dictionnaire universel du XIXe siècle, 1, Pierre Larousse, 1866, pp. 868–73.
- ↑ Ver Charles-Adolphe Wurtz's report on the Karlsruhe Congress.
- ↑ ISO 385:2005 "Laboratory glassware – burettes".
- ↑ El uso del término “solución normal” no es el más recomendado por la IUPAC.
- ↑ International Union of Pure and Applied Chemistry. "{{{title}}}". «Compendium of Chemical Terminology» Internet edition (en inglés).
- ↑ Ver, por ejemplo, Ion Exchange Resins: Classification and Properties, Sigma-Aldrich, http://www.sigmaaldrich.com/etc/medialib/docs/Aldrich/Brochure/al_pp_ionx.pdf, consultado el 14 April 2009.
- Este artículo fue creado a partir de la traducción del artículo Equivalent weight de la Wikipedia en inglés, bajo licencia Creative Commons Atribución Compartir Igual 3.0 y GFDL.
Categorías:- Estequiometría
- Cantidad de sustancia
- Química de polímeros
Wikimedia foundation. 2010.