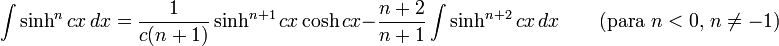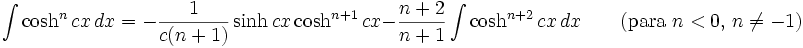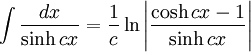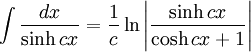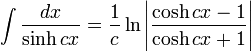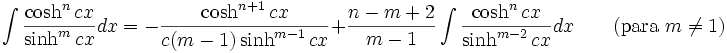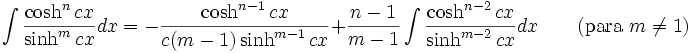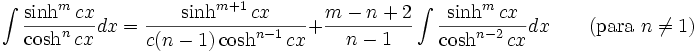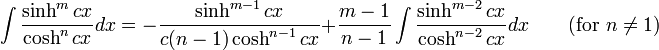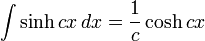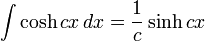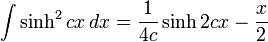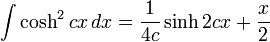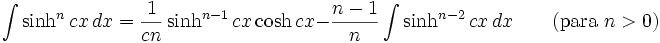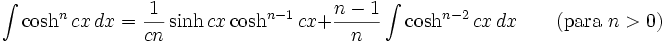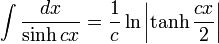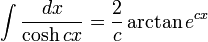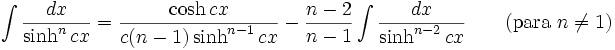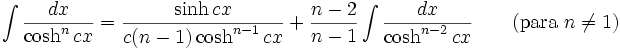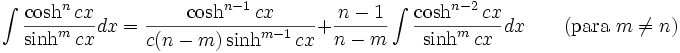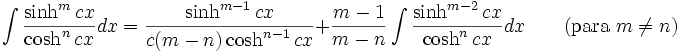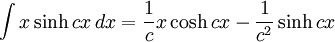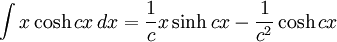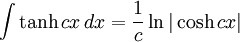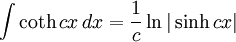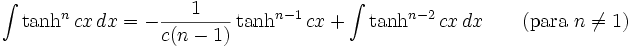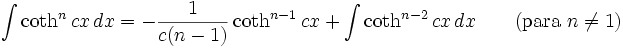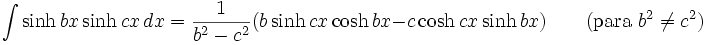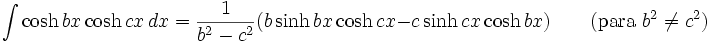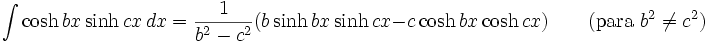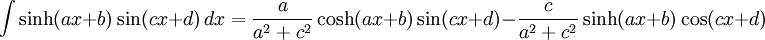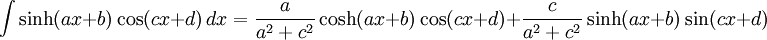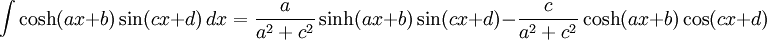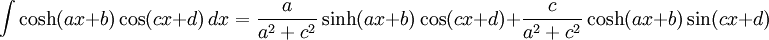Integrales de funciones hiperbólicas

Integrales de funciones hiperbólicas

Anexo:Integrales de funciones hiperbólicas

La siguiente es una lista de integrales de funciones hiperbólicas.

\int\sinh cx\,dx = \frac{1}{c}\cosh cx
\int\cosh cx\,dx = \frac{1}{c}\sinh cx
\int\sinh^2 cx\,dx = \frac{1}{4c}\sinh 2cx - \frac{x}{2}
\int\cosh^2 cx\,dx = \frac{1}{4c}\sinh 2cx + \frac{x}{2}
\int\sinh^n cx\,dx = \frac{1}{cn}\sinh^{n-1} cx\cosh cx - \frac{n-1}{n}\int\sinh^{n-2} cx\,dx \qquad\mbox{(para }n>0\mbox{)}
también: \int\sinh^n cx\,dx = \frac{1}{c(n+1)}\sinh^{n+1} cx\cosh cx - \frac{n+2}{n+1}\int\sinh^{n+2}cx\,dx \qquad\mbox{(para }n<0\mbox{, }n\neq -1\mbox{)}
\int\cosh^n cx\,dx = \frac{1}{cn}\sinh cx\cosh^{n-1} cx + \frac{n-1}{n}\int\cosh^{n-2} cx\,dx \qquad\mbox{(para }n>0\mbox{)}
también: \int\cosh^n cx\,dx = -\frac{1}{c(n+1)}\sinh cx\cosh^{n+1} cx - \frac{n+2}{n+1}\int\cosh^{n+2}cx\,dx \qquad\mbox{(para }n<0\mbox{, }n\neq -1\mbox{)}
\int\frac{dx}{\sinh cx} = \frac{1}{c} \ln\left|\tanh\frac{cx}{2}\right|
también: \int\frac{dx}{\sinh cx} = \frac{1}{c} \ln\left|\frac{\cosh cx - 1}{\sinh cx}\right|
también: \int\frac{dx}{\sinh cx} = \frac{1}{c} \ln\left|\frac{\sinh cx}{\cosh cx + 1}\right|
también: \int\frac{dx}{\sinh cx} = \frac{1}{c} \ln\left|\frac{\cosh cx - 1}{\cosh cx + 1}\right|
\int\frac{dx}{\cosh cx} = \frac{2}{c} \arctan e^{cx}
\int\frac{dx}{\sinh^n cx} = \frac{\cosh cx}{c(n-1)\sinh^{n-1} cx}-\frac{n-2}{n-1}\int\frac{dx}{\sinh^{n-2} cx} \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{dx}{\cosh^n cx} = \frac{\sinh cx}{c(n-1)\cosh^{n-1} cx}+\frac{n-2}{n-1}\int\frac{dx}{\cosh^{n-2} cx} \qquad\mbox{(para }n\neq 1\mbox{)}
\int\frac{\cosh^n cx}{\sinh^m cx} dx = \frac{\cosh^{n-1} cx}{c(n-m)\sinh^{m-1} cx} + \frac{n-1}{n-m}\int\frac{\cosh^{n-2} cx}{\sinh^m cx} dx \qquad\mbox{(para }m\neq n\mbox{)}
también: \int\frac{\cosh^n cx}{\sinh^m cx} dx = -\frac{\cosh^{n+1} cx}{c(m-1)\sinh^{m-1} cx} + \frac{n-m+2}{m-1}\int\frac{\cosh^n cx}{\sinh^{m-2} cx} dx \qquad\mbox{(para }m\neq 1\mbox{)}
también: \int\frac{\cosh^n cx}{\sinh^m cx} dx = -\frac{\cosh^{n-1} cx}{c(m-1)\sinh^{m-1} cx} + \frac{n-1}{m-1}\int\frac{\cosh^{n-2} cx}{\sinh^{m-2} cx} dx \qquad\mbox{(para }m\neq 1\mbox{)}
\int\frac{\sinh^m cx}{\cosh^n cx} dx = \frac{\sinh^{m-1} cx}{c(m-n)\cosh^{n-1} cx} + \frac{m-1}{m-n}\int\frac{\sinh^{m-2} cx}{\cosh^n cx} dx \qquad\mbox{(para }m\neq n\mbox{)}
también: \int\frac{\sinh^m cx}{\cosh^n cx} dx = \frac{\sinh^{m+1} cx}{c(n-1)\cosh^{n-1} cx} + \frac{m-n+2}{n-1}\int\frac{\sinh^m cx}{\cosh^{n-2} cx} dx \qquad\mbox{(para }n\neq 1\mbox{)}
también: \int\frac{\sinh^m cx}{\cosh^n cx} dx = -\frac{\sinh^{m-1} cx}{c(n-1)\cosh^{n-1} cx} + \frac{m-1}{n-1}\int\frac{\sinh^{m -2} cx}{\cosh^{n-2} cx} dx \qquad\mbox{(for }n\neq 1\mbox{)}
\int x\sinh cx\,dx = \frac{1}{c} x\cosh cx - \frac{1}{c^2}\sinh cx
\int x\cosh cx\,dx = \frac{1}{c} x\sinh cx - \frac{1}{c^2}\cosh cx
\int \tanh cx\,dx = \frac{1}{c}\ln|\cosh cx|
\int \coth cx\,dx = \frac{1}{c}\ln|\sinh cx|
\int \tanh^n cx\,dx = -\frac{1}{c(n-1)}\tanh^{n-1} cx+\int\tanh^{n-2} cx\,dx \qquad\mbox{(para }n\neq 1\mbox{)}
\int \coth^n cx\,dx = -\frac{1}{c(n-1)}\coth^{n-1} cx+\int\coth^{n-2} cx\,dx \qquad\mbox{(para }n\neq 1\mbox{)}
\int \sinh bx \sinh cx\,dx = \frac{1}{b^2-c^2} (b\sinh cx \cosh bx - c\cosh cx \sinh bx) \qquad\mbox{(para }b^2\neq c^2\mbox{)}
\int \cosh bx \cosh cx\,dx = \frac{1}{b^2-c^2} (b\sinh bx \cosh cx - c\sinh cx \cosh bx) \qquad\mbox{(para }b^2\neq c^2\mbox{)}
\int \cosh bx \sinh cx\,dx = \frac{1}{b^2-c^2} (b\sinh bx \sinh cx - c\cosh bx \cosh cx) \qquad\mbox{(para }b^2\neq c^2\mbox{)}
\int \sinh (ax+b)\sin (cx+d)\,dx = \frac{a}{a^2+c^2}\cosh(ax+b)\sin(cx+d)-\frac{c}{a^2+c^2}\sinh(ax+b)\cos(cx+d)
\int \sinh (ax+b)\cos (cx+d)\,dx = \frac{a}{a^2+c^2}\cosh(ax+b)\cos(cx+d)+\frac{c}{a^2+c^2}\sinh(ax+b)\sin(cx+d)
\int \cosh (ax+b)\sin (cx+d)\,dx = \frac{a}{a^2+c^2}\sinh(ax+b)\sin(cx+d)-\frac{c}{a^2+c^2}\cosh(ax+b)\cos(cx+d)
\int \cosh (ax+b)\cos (cx+d)\,dx = \frac{a}{a^2+c^2}\sinh(ax+b)\cos(cx+d)+\frac{c}{a^2+c^2}\cosh(ax+b)\sin(cx+d)
Obtenido de "Anexo:Integrales de funciones hiperb%C3%B3licas"

Wikimedia foundation. 2010.

Игры ⚽ Нужна курсовая?

Mira otros diccionarios:

  • Anexo:Integrales de funciones hiperbólicas — La siguiente es una lista de integrales de funciones hiperbólicas …   Wikipedia Español

  • Lista de integrales de funciones hiperbólicas — La siguiente es una lista de integrales de funciones hiperbólicas …   Enciclopedia Universal

  • Integrales de funciones inversas hiperbólicas — Anexo:Integrales de funciones inversas hiperbólicas Saltar a navegación, búsqueda La siguiente es una lista de integrales de las inversas de las funciones hiperbólicas …   Wikipedia Español

  • Anexo:Integrales de funciones inversas hiperbólicas — La siguiente es una lista de integrales de las inversas de las funciones hiperbólicas …   Wikipedia Español

  • Integrales — Anexo:Integrales Saltar a navegación, búsqueda Lista de integrales según el tipo de función: Lista de integrales de funciones racionales Lista de integrales de funciones irracionales Lista de integrales de funciones trigonométricas Lista de… …   Wikipedia Español

  • Anexo:Integrales — Lista de integrales según el tipo de función: Lista de integrales de funciones racionales Lista de integrales de funciones irracionales Lista de integrales de funciones trigonométricas Lista de integrales de funciones hiperbólicas Lista de… …   Wikipedia Español

  • Lista de integrales — según el tipo de función: ● Lista de integrales de funciones racionales ● Lista de integrales de funciones irracionales ● Lista de integrales de funciones trigonométricas ● Lista de integrales de funciones hiperbólicas ● Lista de integrales de… …   Enciclopedia Universal

  • Anexo:Funciones matemáticas — Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas. Puedes añadirlas así o avisar …   Wikipedia Español

  • Fórmulas de reducción para integrales — Anexo:Fórmulas de reducción para integrales Saltar a navegación, búsqueda En ocasiones la integración definida o indefinida de funciones de una variable se facilita mediante las llamadas fórmulas de reducción. Son éstas una cierta forma de poner… …   Wikipedia Español

  • Anexo:Fórmulas de reducción para integrales — En ocasiones la integración definida o indefinida de funciones de una variable se facilita mediante las llamadas fórmulas de reducción. Son éstas una cierta forma de poner en relación integrales que, además de depender de una determinada variable …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”