Un Análogo dimensional del Cubo de Rubik es un rompecabezas cuya geometría y funcionamiento son análogos a los del Cubo de Rubik, es decir puede ser un hipercubo de cualquier número de dimensiones. Estos análogos tienen n^d piezas diferentes, donde d es el número de dimensiones del hipercubo, y n es el número partes en las que se divide cualquiera de las líneas que unen dos vértices del mismo. El conocido cubo de Rubik es un hipercubo con 3³ = 27 piezas cúbicas, de las cuales una es invisible por estar en el centro del cubo.

Estructura

Cada uno de los análogos tiene sus piezas cubiertas por estampitas de colores, las cuales tienen d − 1 dimensiones. Sin embargo, sólo un subconjunto de las piezas muestran sus estampitas al exterior, es decir hay piezas con un distinto número de estampitas visibles en d dimensiones. Por ejemplo, en el Cubo de Rubik existen piezas que tienen 0, 1, 2, y 3 estampitas. En general los análogos contienen d + 1 tipos distintos de piezas. Para cada tipo distinto de piezas se puede conocer el número total de ellas en el rompecabezas a través de la fórmula

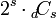
Donde d es el número de dimensiones, s es el número de estampitas de un tipo de pieza particular, y 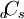es el número de combianaciones de d cosas tomadas en s, lo que es igual a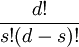

Si añadimos a nuestra fórmula el operador n − 2 obtenemos una expresion para el número de piezas de cualquier n, d, y s

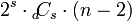
A partir de estos planteamientos podemos deducir el número de piezas de todos los tipos, por ejemplo de un análogo de la forma 3^d: