Punto al infinito

Punto al infinito

Punto al infinito

El punto al infinito o punto en el infinito es una entidad topológica y geométrica que se introduce a modo de cierre o frontera infinita del conjunto de los números reales.

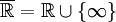
\overline{\mathbb{R}} = \mathbb{R} \cup \{\infty\}

Para que el punto en el infinito represente efectivamente el infinito real se define en 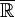\overline{\mathbb{R}} la topología 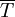\overline{T} formada por todos los conjuntos:

  • A que son abiertos de \mathbb{R}
  • B que son complementarios de conjuntos compactos (cerrados y acotados) de \mathbb{R} .

Los conjuntos A son los abiertos de 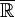\overline{\mathbb{R}} que no contienen el 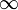\infty mientras que los conjuntos B son los que sí lo contienen.

Sea 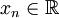x_n\in\mathbb{R} una sucesión de números reales tales que 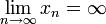\lim_{n \to \infty}x_n = \infty. Dentro del conjunto de los números reales, esto quiere decir únicamente que:

\forall K><span class=0\ \exists m\in \mathbb{N} | si\ n>m \Rightarrow x_n \notin [-K,K]" style="max-width : 98%; height: auto; width: auto;" src="/pictures/eswiki/49/19ea9c5dfa3b8188538f5fc9ce8341bb.png">

Pero esta misma condición implica en 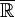\overline{\mathbb{R}} que

\forall B|\infty\in B \ \exists m\in N | si\ n><span class=m \Rightarrow x_n\in B" style="max-width : 98%; height: auto; width: auto;" src="/pictures/eswiki/102/fc8b3592dcdcaa07f15ec3e57212d129.png">

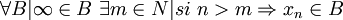
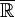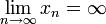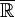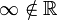es decir que en \overline{\mathbb{R}} se escribe también \lim_{n \to \infty}x_n = \infty. Sin embargo, sólo en \overline{\mathbb{R}} se puede decir que la sucesión xn converge, puesto que \infty\notin \mathbb{R}.

Obtenido de "Punto al infinito"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать курсовую

Mira otros diccionarios:

  • Infinito — El símbolo de infinito ∞ (Unicode U+221E), también llamado lemniscata, en diferentes fuentes. Para el canal de televisión por cable, véase Infinito (canal de televisión). El concepto de infinito aparece en varias ramas de la filosofía …   Wikipedia Español

  • Punto de fuga — Saltar a navegación, búsqueda El punto de fuga, en un sistema de proyección cónica, es el lugar donde convergen todas las rectas proyectadas paralelas a una dirección; es un punto situado en el infinito. Existen tantos puntos de fuga como… …   Wikipedia Español

  • Punto remoto — Saltar a navegación, búsqueda En Óptica, Optometría y Oftalmología, es el punto en el cual un paciente ve nítido sin necesidad de acomodar su cristalino, es decir, de no contraer su cristalino para ver correctamente. En los miopes, el punto… …   Wikipedia Español

  • Infinito — (Del lat. infinitus.) ► adjetivo 1 Que no tiene fin: ■ la capacidad de la imaginación humana es infinita; el universo es infinito. SINÓNIMO interminable ANTÓNIMO finito 2 Que es muy grande o numeroso: ■ su sabiduría es infinita; se equivocó… …   Enciclopedia Universal

  • Número infinito — El concepto del infinito aparece en varias ramas de las matemáticas, entre otras en la geometría (punto al infinito de la geometría proyectiva), en el análisis (límites infinitos, o límites al infinito) y en los números (números ordinales y… …   Enciclopedia Universal

  • Nudo Infinito — El Nudo Infinito o eterno es un nudo simbólico usado en el Budismo Tibetano. El nudo infinito. Dado que el nudo no tiene principio ni fin, simboliza la infinita sabiduría de Buda. El mismo motivo puede encontrarse en el arte chino como uno de los …   Wikipedia Español

  • IEEE punto flotante — Saltar a navegación, búsqueda El estándar de la IEEE para aritmética en coma flotante (IEEE 754) es el estándar más extendido para las computaciones en punto flotante, y es seguido por muchas de las mejoras de CPU y FPU. El estándar define… …   Wikipedia Español

  • Guerra del Infinito — La guerra del Infinito es una serie limitada de seis números publicada por Marvel Comics en 1992. Escrita por Jim Starlin e ilustrada por Ron Lim, es la segunda parte de la llamada Trilogía del Infinito (que se completa con el Guantelete del… …   Wikipedia Español

  • IEEE punto flotante — El estándar de la IEEE para aritmética en coma flotante (IEEE 754) es el estandard mas ampliamente usado para la para las computaciones en punto flotante, y es seguida por muchas de las implementaciones de CPU y FPU. El estandard define formatos… …   Enciclopedia Universal

  • Fracción continua generalizada — Saltar a navegación, búsqueda En análisis complejo, una rama de las matemáticas, una fracción continua generalizada o fracción fractal es una generalización de una fracción continua en la cual los numeradores parciales y los denominadores… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
https://es-academic.com/dic.nsf/eswiki/972873 Do a right-click on the link above
and select “Copy Link”