Recta tangente

Recta tangente

Recta tangente

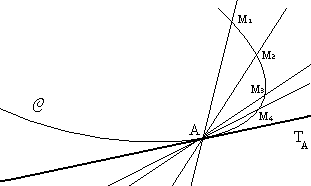
Cuerdas.png

Sea C una curva, y A un punto de esta. Se supone que A es un punto regular de la curva, es decir que no es un punto anguloso: La curva no cambia repentinamente de dirección en A.

La tangente a C en A es la recta TA que pasa por A y que tiene la misma dirección que C alrededor de A.

La tangente es la posición límite de la recta (AM) (llamada cuerda de la curva), cuando M es un punto de C que se aproxima indefinidamente al punto A (M se desplaza sucesivamente por M1, M2, M3, M4...)

Si C representa una función f (no es el caso en el gráfico precedente), entonces la recta (AM) tendrá como coeficiente director (o pendiente)

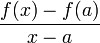\frac {f(x) - f(a)} {x - a}, donde a es la abscisa de A y x la de M.

Por lo tanto, la pendiente de la tangente TA será:

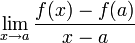
\lim_{x \to a} \frac {f(x) - f(a)} {x - a}

Es, por definición, f '(a), la derivada de f en a.

La ecuación de la tangente es Ta: y = f '(a)·(x - a) + f(a)

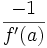La recta ortogonal a la tangente TA que pasa por el punto (a, f(a)) se denomina recta normal y su pendiente, en un sistema de coordenadas ortonormales, es dada por \frac {-1} {f'(a)}.
Su ecuación es : y = - (x - a)/f '(a) + f(a) suponiendo claro está que f'(a) ≠ 0. Esta recta no interviene en el estudio general de las funciones pero sí en problemas geométricos relacionados con las cónicas, como por ejemplo para determinar el punto focal de una parábola.

Obtenido de "Recta tangente"

Wikimedia foundation. 2010.

Игры ⚽ Поможем написать реферат

Mira otros diccionarios:

  • tangente — (Del ant. part. act. de tangir; lat. tangens, entis). 1. adj. Que toca. 2. Geom. Dicho de dos o más líneas o superficies: Que se tocan o tienen puntos comunes sin cortarse. 3. f. Geom. Recta que toca a una curva o a una superficie sin cortarlas.… …   Diccionario de la lengua española

  • Tangente (geometría) — Este artículo trata sobre el concepto en geometría. Para otros usos de este término, véase tangente (trigonometría). en verde: línea tangente en azul: línea secante en rojo: cuerda Tangente proviene del latín «tangens»=que toca …   Wikipedia Español

  • Tangente — (Del lat. tangens, tis.) ► adjetivo 1 Que toca o está en contacto con alguna cosa o idea: ■ sus posturas son tangentes pero no iguales. SINÓNIMO tocante 2 GEOMETRÍA Se aplica a la línea o a la superficie que toca o tiene algún punto en común con… …   Enciclopedia Universal

  • Tangente — En matemáticas, tangente puede referirse a: Tangente (trigonometría). Tangente (geometría). Véase también Tangente hiperbólica. Tangencias (una ampliación gráfica de la página tangente). Recta tangente (para un análisis unidimensional). Espacio… …   Wikipedia Español

  • Recta secante — Para la razón trigonométrica recíproca del coseno, véase secante (trigonometría). Recta secante que corta una circunferencia …   Wikipedia Español

  • tangente — 1 s f y adj m y f (Geom) Línea o superficie que tiene un punto en común con una línea o superficie curva sin que se corten entre sí: la tangente de una circunferencia, recta tangente, círculos tangentes 2 s f (Mat) Con respecto a un ángulo,… …   Español en México

  • Recta de altura — Saltar a navegación, búsqueda La recta de altura es la línea de posición por excelencia usada en navegación astronómica, descubierta por casualidad en 1837 por el capitán Thomas H. Sumner.[1] La recta de altura, es en realidad una aproximación al …   Wikipedia Español

  • Recta — Para otros usos de este término, véase Recta (desambiguación). Se ha sugerido que Línea sea fusionado en este artículo o sección (discusión). Una vez que hayas realizado la fusión de artículos, pide la fusión de historiales aquí …   Wikipedia Español

  • Recta — ► sustantivo femenino 1 GEOMETRÍA Línea que une dos puntos. 2 Parte de una carretera o de un circuito trazados como esta línea. FRASEOLOGÍA recta de llegada DEPORTES La última antes de llegar a la meta, en algunos deportes. * * * recta f. Línea… …   Enciclopedia Universal

  • tangente — {{＃}}{{LM T37098}}{{〓}} {{［}}tangente{{］}} ‹tan·gen·te› {{《}}▍ adj.inv./s.f.{{》}} {{＜}}1{{＞}} {{♂}}En geometría, referido a una línea o a una superficie,{{♀}} que tocan otras líneas o superficies o que tienen puntos en común con ellas sin… …   Diccionario de uso del español actual con sinónimos y antónimos

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”