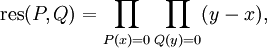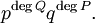Resultante

Resultante

Resultante

En matemáticas, la resultante de dos polinomio mónico P y Q sobre un cuerpo k se define como el producto:

\mathrm{res}(P,Q) = \prod_{P(x)=0} \prod_{Q(y)=0} (y-x),\,

de las diferencias de sus raíces, donde x y y toma valores en la clausura algebraica de k. Para polinomios no mónicos con coeficientes dominantes p y q, respectivamente, el producto de más arriba se multiplica por

p^{\deg Q} q^{\deg P}.\,

Contenido

Computación

  • La resultante es el determinante de la matriz de Sylvester.
  • El productorio anterior puede ser reescrito como
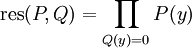
\mathrm{res}(P,Q) = \prod_{Q(y)=0} P(y)\,
y esta expresión permanece invariante si P se reduce módulo Q.
  • Sea 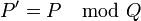P' = P \mod Q. La idea anterior puede ser aplicada intercambiando los papeles de P' y Q. Sin embargo, P' tiene un conjunto de raíces diferentes de las de P. Esto puede ser resuelto escribiendo 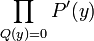\prod_{Q(y)=0} P'(y)\, como un determinante otra vez, donde P' tiene como coeficientes no dominantes el cero. Este determinante puede ser simplificado mediante una expansión iterativa con respecto la columna, donde solo el coeficiente dominante q de Q aparece.
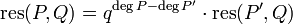
\mathrm{res}(P,Q) = q^{\deg P - \deg P'} \cdot \mathrm{res}(P',Q)
Continuando este procedimiento obtenemos una variante del algoritmo de Euclides. Este procedimiento necesita tiempo de ejecución cuadrático.

Propiedades

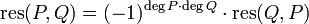
  • \mathrm{res}(P,Q) = (-1)^{\deg P \cdot \deg Q} \cdot \mathrm{res}(Q,P)
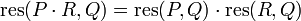
  • \mathrm{res}(P\cdot R,Q) = \mathrm{res}(P,Q) \cdot \mathrm{res}(R,Q)
  • Si P' = P + R * Q y degP' = degP, entonces res(P,Q) = res(P',Q)
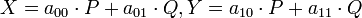  • Si X,Y,P,Q tienen el mismo grado y X = a_{00}\cdot P + a_{01}\cdot Q, Y = a_{10}\cdot P + a_{11}\cdot Q,
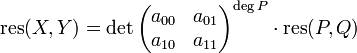
entonces \mathrm{res}(X,Y) = \det{\begin{pmatrix} a_{00} & a_{01} \\ a_{10} & a_{11} \end{pmatrix}}^{\deg P} \cdot \mathrm{res}(P,Q)
  • res(P − ,Q) = res(Q − ,P) donde P − (z) = P( − z)

Aplicaciones

  • Las resultantes pueden ser usadas en la geometría algebraica para determinar intersecciones. Por ejemplo, sean f(x,y) = 0 y g(x,y) = 0 definiendo unas curva algebraica en 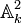\mathbb{A}^2_k. Si f y g son vistos como polinomios en x con coeficientes en k(y), entonces la resultante de f y g es un polinomio en y cuyas raíces son las coordenadas y de la intersección de las curvas.

Referencias

Obtenido de "Resultante"

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

  • Resultante [1] — Resultante eines Systems von n Gleichungen in n Veränderlichen ist eine ganze Funktion der Koeffizienten, die verschwinden muß, wenn die gegebenen Gleichungen ein gemeinsames Wertesystem der Veränderlichen haben sollen. Die Resultante ändert sich …   Lexikon der gesamten Technik

  • résultante — [ rezyltɑ̃t ] n. f. • 1652; de résultant ♦ Sc. Somme géométrique de deux ou plusieurs vecteurs. La résultante de deux forces. Transformation géométrique équivalente à des transformations appliquées successivement. ⇒ produit. ♢ Cour. Conséquence,… …   Encyclopédie Universelle

  • Resultante [2] — Resultante von Bewegungen und Kräften ist eine Bewegung oder Kraft, die denselben Effekt wie eine Reihe gleichzeitig wirkender Bewegungen oder Kräfte hervorbringt. Erfährt ein Punkt gleichzeitig zwei Verschiebungen oder wirken zwei Kräfte an ihm …   Lexikon der gesamten Technik

  • resultante — adj. 2 g. 1. Que resulta. 2. Relativo ao resultado da composição de todos os elementos de um sistema. • s. f. 3.  [Física] Vetor único (se existir) que equivale a um sistema de vetores deslizantes. (Os vetores concorrentes têm sempre uma… …   Dicionário da Língua Portuguesa

  • resultante — Cuando este adjetivo se sustantiva, tomando el sentido de ‘elemento que resulta de otros varios’, se usa en ambos géneros, con predominio del femenino, especialmente en el ámbito de la física y las matemáticas: «Si al desplazarse el cuerpo existe …   Diccionario panhispánico de dudas

  • Resultánte — (lat.), s. Parallelogramm …   Kleines Konversations-Lexikon

  • resultante — adjetivo,sustantivo femenino 1. Área: física [Fuerza] que equivale al conjunto de otras fuerzas …   Diccionario Salamanca de la Lengua Española

  • resultante — (Del ant. part. act. de resultar). 1. adj. Que resulta. 2. Fís. Se dice de la suma geométrica de dos o más vectores. U. t. c. s. f.) …   Diccionario de la lengua española

  • Resultante — In der Mathematik ist die Resultante ein Werkzeug der kommutativen Algebra, um zwei Polynome auf das Vorhandensein gemeinsamer Nullstellen zu prüfen. In Erweiterung auf multivariate polynomiale Gleichungssysteme kann die Resultante dazu verwendet …   Deutsch Wikipedia

  • resultante — ► adjetivo 1 Que resulta o procede de una cosa: ■ el beneficio resultante es de dos millones. ► adjetivo/ sustantivo femenino 2 MATEMÁTICAS Se aplica a la fuerza o vector que produce los mismos efectos que un conjunto de fuerzas o vectores. * * * …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”