Un cuerpo o campo es un anillo de división conmutativo, es decir, un anillo conmutativo en el que todo elemento distinto de cero (todo elemento no nulo) es invertible respecto del producto (es una unidad).

Ejemplos: el cuerpo de los números racionales 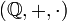, el de los reales 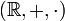, o el de los complejos 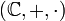. Donde el símbolo "+" representa la operación de suma, y el símbolo "·" representa la operación de multiplicación.

En álgebra abstracta, un cuerpo es una estructura algebraica en la cual las operaciones de adición y multiplicación se pueden realizar y cumplen las propiedades asociativa, conmutativa y distributiva, además de la existencia de un inverso aditivo y de un inverso muliplicativo, los cuales permiten efectuar la operaciones de substracción y división (excepto la división por cero); estas propiedades ya son familiares de la aritmética de números ordinarios.

Los cuerpos son objetos importantes de estudio en álgebra puesto que proporcionan la generalización apropiada de dominios de números tales como los conjuntos de números racionales, de los números reales, o de los números complejos. Los cuerpos eran llamados dominios racionales.

El concepto de un cuerpo se usa, por ejemplo, al definir el concepto de espacio vectorial y las transformaciones en estos objetos, dadas por matrices, dos objetos en el álgebra lineal cuyos componentes pueden ser elementos de un cuerpo arbitrario. La teoría de Galois estudia las relaciones de simetría en las ecuaciones algebraicas, desde la observación del comportamiento de sus raíces y las extensiones de cuerpos correspondientes y su relación con los automorfismos de cuerpos correspondientes.

Contenido 1 Definición 1.1 Subcuerpos e ideales 2 Propiedades de los cuerpos 3 Ejemplos de cuerpos 4 Algunos teoremas iniciales 5 Construyendo nuevos cuerpos de otros dados

Definición

Un cuerpo es un anillo conmutativo (F, +, *) tal que 0 es distinto de 1 y todos los elementos de F salvo 0 tienen inverso multiplicativo.

Explicado, esto significa que vale lo siguiente:

F es cerrado para las operaciones + y *:

Para toda a, b en F, a + b y a * b pertenecen a F (o más formalmente, + y * son operación binaria en F);

Ambas + y * son asociativas:

Para toda a, b, c en F, a + (b + c) = (a + b) + c y a * (b * c) = (a * b) * c.

Ambas + y * son conmutativos:

Para toda a, b en F, a + b = b + a y a * b = b * a.

La operación * es distributiva sobre la operación +:

Para toda a, b, c, en F, a * (b + c) = (a * b) + (a * c).

Existencia de un elemento neutro para +:

Existe un elemento 0 en F, tal que para todo a en F, a + 0 = a.

Existencia de un elemento neutro para *:

Existe un elemento 1 en F diferente a 0, tal que para todo a en F, a * 1 = a.

Existencia de elemento opuesto:

Para cada a en F, existe un elemento -a en F, tal que a + (- a) = 0.

Existencia de inversos:

Para cada a ≠ 0 en F, existe un elemento a ^-1 en F, tal que a * a^-1 = 1.

El requisito 0 ≠ 1 asegura que el conjunto que contiene solamente un cero no sea un cuerpo, y de paso elimina la posibilidad de que en el cuerpo existan divisores de cero distintos de 0. Directamente de los axiomas, se puede demostrar que (F, +) y (F - { 0 }, *) son grupos conmutativos y que por lo tanto (véase la teoría de grupos) el opuesto -a y el inverso a^-1 son determinados únicamente por a. Además, el inverso de un producto es igual al producto de los inversos:

(a*b)^-1 = a^-1 * b^-1

con tal que a y b sean diferentes de cero. Otras reglas útiles incluyen

-a = (-1) * a

y más generalmente

- (a * b) = (-a) * b = a * (-b)

así como

a * 0 = 0,

todas reglas familiares de la aritmética elemental.

Subcuerpos e ideales

Sea 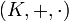un cuerpo, y 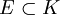. Se dice que E es subcuerpo de K o que K es extensión de E si se cumple que 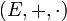es un cuerpo cuando las operaciones + y se restringen a E. En particular E será entonces subanillo de 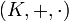. Se tiene entonces que (E, + ) y 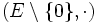son subgrupos respectivos de los grupos abelianos (K, + ) y .

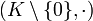Como todo cuerpo es un anillo, podríamos preguntarnos por la forma que tengan sus ideales. Para empezar, como todo cuerpo es anillo conmutativo, todo ideal por la izquierda es ideal (bilátero) y todo ideal por la derecha es también ideal (bilátero). Así pues sólo hemos de estudiar los ideales del cuerpo. Si I es ideal del cuerpo K, entonces todo elemento no nulo 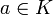ha de tener inverso 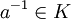, luego a es una unidad de K (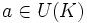), y se tendrá que 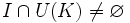, i.e., I = R. De esta manera, los únicos ideales de un cuerpo son el propio cuerpo y el ideal nulo.

Propiedades de los cuerpos

• Todo cuerpo es dominio de integridad
• Si 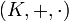es un cuerpo, entonces, 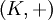y 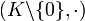son grupos abelianos

Ejemplos de cuerpos

• Los números racionales 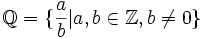donde está incluido el conjunto 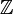de los números enteros.

• Los números reales .

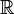• Los números complejos .

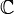• El cuerpo más pequeño tiene solamente dos elementos: 0 y 1. Es denotado por 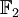o 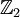y puede a veces ser definido por las dos tablas

     +  0  1        *  0  1
     0  0  1        0  0  0
     1  1  0        1  0  1

Tiene aplicaciones importantes en informática, especialmente en criptografía y teoría de la codificación.

• Más generalmente, para un número primo p, el conjunto de los números enteros módulo p es un cuerpo finito con los p elementos: esto se escribe a menudo como 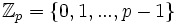donde las operaciones son definidas realizando la operación en 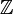, dividiendo por p y tomando el resto, ver aritmética modular.

• Los números reales contienen varios subcuerpos interesantes: los números reales algebraicos, los números computables, y los números definibles.

• Los números complejos contienen el cuerpo de números algebraicos, la clausura algebraica de Q.

• Los números racionales se pueden ampliar a los cuerpos de números p-ádicos para cada número primo p.

• Sean E y F dos cuerpos con E un subcuerpo de F (es decir, un subconjunto de F que contiene 0 y 1, cerrado bajo las operaciones + y * de F y con sus propias operaciones definidas por restricción). Sea x un elemento de F no en E. Entonces E(x) se define como el subcuerpo más pequeño de F que contiene a E y a x. Por ejemplo, Q(i) es el subcuerpo de los números complejos C que consisten en todos los números de la forma a+bi donde a y b son números racionales.

• Para un cuerpo dado F, el conjunto F(x) de funciones racionales en la variable X con coeficientes en F es un cuerpo; esto se define como el conjunto de cocientes de polinomios con coeficientes en F.

• Si F es cuerpo, y p(X) es un polinomio irreducible en un anillo de polinomios F[X], entonces el cociente F[X]/<p(X)> es un cuerpo con un subcuerpo isomorfo a F. Por ejemplo, es un cuerpo (de hecho, es isomorfo al cuerpo de los números complejos).

• Cuando F es un cuerpo, el conjunto F((x)) de series formales de Laurent sobre F es un cuerpo.

• Si V es una variedad algebraica sobre F, entonces las funciones racionales V → F forman un cuerpo, el cuerpo de funciones V.

• Si S es una superficie de Riemann, entonces las funciones meromorfas de S → C forman un cuerpo.

• Si I es un conjunto de índices, U es un ultrafiltro sobre I, y F_i es un cuerpo para cada i en I, el ultraproducto de F_i (usando U) es un cuerpo.

• Los números hiperreales forman un cuerpo que contiene los reales, más los números infinitesimales e infinitos.

• Los números surreales forman un cuerpo que contiene los reales, a excepción del hecho de que son una clase propia, no un conjunto. El conjunto de todos los números surreales con el cumpleaños menor que un cierto cardinal inaccesible es un cuerpo.

• Los nimbers forman un cuerpo, otra vez a excepción del hecho de que son una clase propia. El conjunto de nimbers con el cumpleaños menor que 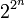, los nimbers con el cumpleaños menor que cualquier cardinal infinito son todos ejemplos de cuerpos.

Algunos teoremas iniciales

• El conjunto de elementos diferentes de cero de un cuerpo F (denotado típicamente por F^×) es un grupo abeliano bajo multiplicación. Cada subgrupo finito de F^× es cíclico.

• La característica de cualquier cuerpo es cero o un número primo. (la característica se define como el número entero positivo más pequeño n tal que n·1 = 0, o cero si no existe tal n; aquí n·1 significa n sumandos 1 + 1 + 1 +... + 1.)

• Si q > 1 es una potencia de un número primo, entonces existe (salvo isomorfismo) exactamente un cuerpo finito con q elementos. Además, estos son los únicos cuerpos finitos posibles.

• Como anillo, un cuerpo no tiene ningún ideal excepto {0} y sí mismo.

• Todo anillo de división finito es un cuerpo (teorema de Wedderburn)

• Para cada cuerpo F, existe (salvo isomorfismo) un cuerpo único G que contiene a F, es algebraico sobre F, y es algebraicamente cerrado. G se llama la clausura algebraica de F.

Construyendo nuevos cuerpos de otros dados

• Si un subconjunto E de un cuerpo (F,+,*) junto con las operaciones *, + restringido a E es en sí mismo un cuerpo, entonces se llama un subcuerpo de F. Tal subcuerpo tiene los mismos 0 y 1 que F.

• Dado un cuerpo F, el cuerpo polinómico F(X) es el cuerpo de fracciones de polinomios en X con coeficientes en F, es decir, sus elementos son funciones racionales con coeficientes en F.

• Una extensión algebraica de un cuerpo F es el cuerpo más pequeño que contiene a F y una raíz de un polinomio irreducible p(X) en F [X]. Alternativamente, es idéntico al anillo factor F [X]/<p(X)>, donde <p(X)> es el ideal generado por p(X).