- Rosa polar
-
Rosa polar
En matemáticas, rosa polar es el nombre que recibe cualquier miembro de una familia de curvas de ecuación
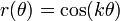 por asemejarse a una flor de pétalos.
por asemejarse a una flor de pétalos.Esta familia, también conocida como rhodoneas (del griego rhodon, rosa), fue estudiada por el matemático Luigi Guido Grandi, en torno al 1725, en su libro Flores Geometrici.[1]
Como casos particulares, la rosa de tres pétalos recibe también el nombre de trifolium regular y la de cuatro, el de quadrifolium. Para k=1/2 se obtiene la curva conocida como folium de Durero.
Contenido
Ecuación
Su expresión general en coordenadas polares es:
Donde a representa la longitud de los pétalos y φ0 sólo tiene un efecto de realizar una rotación global sobre la figura. Salvo similaridad, todas estas curvas pueden reducirse a la familia:
Aquí la forma queda determinada por el valor del parámetro k:
- Si k es un número entero, estas ecuaciones producirán k pétalos si k es impar, o 2k pétalos si k es par.
- Si k is racional, entonces la curva es cerrada y de longitud finita.
- Si k es irracional, su imagen formará un conjunto denso en el disco de radio a.
La expresión en coordenadas cartesianas de la rosa de cuatro pétalos es (x2 + y2)3 = 4a2x2y2 y para la rosa de tres pétalos (x2 + y2)2 = ax(x2 − 3y2).
Área
El área de una rosa de ecuación
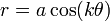 con k natural es igual a:
con k natural es igual a:si k es par, y
si k es impar.
Notas y referencias
Enlaces externos
- Rosa en Mathworld
- Applet para crear rosas con parámetro k
- Diccionario visual de curvas planas especiales Xah Lee
- Extraído de Wikipedia en Inglés
Categorías: Curvas | Figuras geométricas
Wikimedia foundation. 2010.



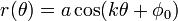

 (θ) = 2 sin 4θ. Su área es, sorprendentemente, la mitad de la del círculo en que está inscrita.
(θ) = 2 sin 4θ. Su área es, sorprendentemente, la mitad de la del círculo en que está inscrita.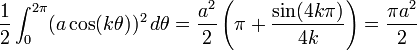
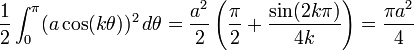
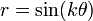 y
y 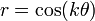 representa la misma curva salvo una rotación de π/2k radianes.
representa la misma curva salvo una rotación de π/2k radianes.