Salario Hedónico

Salario Hedónico: Salario Hedónico

Saltar a navegación, búsqueda

Los salarios hedónicos son definidos como el precio implícito – del trabajo – de los atributos que revelan los agentes económicos de los precios observados de diferentes productos y de una cantidad específica de características asociados a ellos (Rosen, 1974). Este diferencial en los precios refleja la valoración económica que los trabajadores (firma) asignan a las características que el trabajo (trabajador) posee (Vásquez, 2006).

Hasta este punto es necesario esclarecer el sentido del concepto de mercado implícito. Se refiere al bien que se transa por consecuencia de comerciar con un bien que ya incluye al bien anterior.

Como ejemplo, el caso más común dentro del método de los precios hedónicos (MPH) es el mercado de las propiedades residenciales. Entonces, en este mercado no sólo se transan las casas en juego, sino también, “implícitamente” se encuentra el mercado del paisaje del entorno de las casas, el mercado del clima de la zona residencial, el mercado de la ubicación residencial, etc. Por lo que siendo un poco más específico, el mercado implícito de refiere al mercado de las característica de los bienes transados.

Por otro lado, dentro de esta teoría se maneja el concepto de “amenidad” que se refiere al conjunto de características que potencia el valor de las características de los bienes en cuestión, ie., en lenguaje sencillo, las buenas características. Inversamente, las “desamenidades” son las que afectan negativamente el valor de estos bienes.

Ahora bien, en el tema de los salarios hedónicos (Mercado Laboral) reside la peculiaridad en que existen dos puntos de vista importantes. Cuando se trata, e.g., de el mercado de los bienes raíces, automóviles e incluso bienes ambientales, suponemos que el consumidor asigna una valoración diferente a cada característica del bien, pero el vendedor del bien (o la contraparte del tratado comercial) no exige características del comprador.

Sin embargo, en el mercado laboral, las características que posea el empleo son las que asignan implícitamente el salario exigido por el trabajador y, análogamente, las características del trabajador son las que definen implícitamente el salario ofrecido por el empleador.

Contenido

1 Referencia Histórica

2 Teoria

2.1 Preferencias del Trabajador

2.2 Oferta de Mercado

2.3 Elección de la Firma

2.4 Demanda de Mercado

2.5 Equilibrio en los Mercados

3 Conclusión

4 Referencias

Referencia Histórica

Los salarios hedónicos son el caso especial de la teoría que estudia los precios hedónicos. Hoy en día la aplicación de este método alcanza también el tema de la valoración económica. Una clara contextualización histórica se encuentra en el libro de Vásquez (2006) donde comenta que el método original fue aplicado primitivamente por Hass (1922), aunque se dice que éste influenció los trabajos de Wallace (1926), que es más conocido por este aporte que el mismo Hass.

Aunque Taylor en su trabajo “The Hedonic Method” sitúa su origen en Wuagh (1928) , y Griliches (1961) se lo atribuye a Court (1939).

En lo que si no hay discusión es en que Rosen (1974) realiza el aporte más importante en este campo en un contexto de equilibrio parcial y una ampliación de la teoría la realiza Jeniffer Roback (1982) en un modelo de equilibrio general. De las aplicaciones más significativas se encuentra el magro trabajo de Jin-Tan Liu et al (1997) que es el primero en aplicar el método de salarios hedónicos a un país en vías de desarrollo como Taiwan. Se concentró entre 1982 y 1986 enfocándose en la relación riesgo-salario.

Teoria

En el mercado laboral se observa que los trabajadores simultáneamente venden sus servicios de trabajo e instantáneamente compran los atributos de este trabajo. Y estos atributos son fijos en todos los trabajos, pero varían de trabajo en trabajo. Por otro lado los empleadores simultáneamente compran los servicios y las características de los trabajadores y venden los atributos de sus trabajos ofrecidos en el mercado. Estas características que compran son fijas en cada trabajador pero pueden variar de trabajador en trabajador.

Ahora, el ajuste ocurre cuando las elecciones de preferencias de un empleado y un empleador son simultáneamente consistentes, i.e., cuando un trabajador encuentra los atributos de un trabajo deseables y el empleador encuentra las características productivas del trabajador que desea, y ambas son elecciones factibles.

Por lo que el Trabajo de una economía es, finalmente, la suma de dos transacciones conceptualmente diferentes, por un lado, por los servicios y características del trabajador, y por otro por las características del trabajo. Otra forma de verlo, es que el trabajador paga una cantidad positiva por poder trabajar en un cierto trabajo con amenidades, el cual es restado de su salario pagado. Mientras que por el lado del contratador, este debe pagar una suerte de salario Premium para que los trabajadores estén dispuestos a realizar actividades onerosas y es por eso que el mercado laboral, como se comentó en el apartado anterior, es un mercado implícito de los atributos de los trabajadores y puestos de trabajo.

El resultado en este mercado es un equilibrio asociado a un salario para cada asignación, y el conjunto de salarios, atributos y características asociadas a todas las asignaciones son igualaciones de diferencias en los mercados. Estas igualaciones de diferencias son los diferenciales de salario observados requeridos para ecualizar las ventajas y desventajas, monetarias y no monetarias, que existen a través de los trabajos y de los trabajadores (Rosen, 1986). Estas diferencias de precio a través de los salarios reflejan la valoración económica por las características en juego, aunque no completamente como se observará más adelante. Veamos un ejemplo al estilo de Friedman y Kuznets (1954). Utilizaremos su nomenclatura y su punto de vista. Para esto suponemos un mercado laboral donde los trabajadores tienen productividad homogénea y existen solo dos tipos de trabajos.

Si $D$ es el índice de amenidad, decimos que $D = 1$ cuando el trabajo tiene desamenidades, como pueden ser aire contaminado, trabajo a la intemperie, peligro de sufrir daño físico, etc. Diremos que $D = 0$ cuando el trabajo presenta amenidades, como una cómoda oficina con aire acondicionado, ventanas amplias, ubicado en una ciudad tranquila, etc. Entonces, como a priori estamos revisando la versión general de la teoría de salarios hedónicos, podemos hacer una clasificación general de las variables (sugeridas) y supuestos del modelo. Decimos que:

Cada trabajador es clasificado según su tipo (basado en algún tipo de medición objetiva).

Existen dos tipos de salarios pagados por cada tipo de trabajo, $w 0$ y $w 1$ (el subíndice hace referencia al índice de amenidad).

Los datos asociados a cada trabajador son:

El ingreso no monetario de este.

Estatus familiar.

Mediciones de su calidad de salud.

Edad.

Otras variables demográficas.

Por el lado de la firma, los datos son:

Tamaño de la firma.

Tipo de industria.

Intensidad de capital.

Finalmente, el problema es construir un modelo econométrico estructural que describa cómo estos datos son generados. Para ello nos enfocamos en presentar la forma en que el consumidor y la firma buscan sus propios óptimos y cómo, luego, estos se ajustan a través de la interacción del mercado. Recordamos que esta en una versión general presentada por Rosen (1974). En un momento más me explayaré en una versión más específica del modelo.

Preferencias del Trabajador

Las preferencias de los trabajadores son representadas a través de la siguiente función de utilidad:
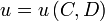
$u = u \left( C , D \right)$
Donde $C$ es el consumo de bienes por medio del dinero y $D$ es el indicador del consumo de un trabajador, obviamente asociado al tipo de trabajo que posee, con o sin amenidades. Por lo tanto, es obvio suponer que:
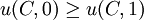
$u ( C , 0 ) \geq u ( C , 1 )$
Esto nos dice que un trabajo, dado un mismo consumo, entrega más utilidad al trabajador cuándo este trabajo presenta amenidades, que cuándo no las presenta o son desamenidades.

Y con esta función se puede calcular cómo el ingreso, o el consumo de mercado, debe ser compensado para aceptar un trabajo menos preferido.

Si $C 0$ es el nivel de consumo cuando $D = 0$ , dado un $C = 0$ , definimos $C *$ como el nivel de consumo requerido para alcanzar la misma utilidad en un caso $D = 1$ . Entonces $C *$ satisface $u (C * ,1) = u (C 0,0)$ Como $C * > = C 0$ ya que $D = 1$ nunca es preferido en forma natural a $D = 0$ , definimos la diferencia $Z = C * - C 0$

Y ésta será la variación compensada para $D = 1$ comparado con $D = 0$ , que quiere decir que ésta es la compensación necesaria para hacer que el trabajador sea indiferente entre los dos tipos de trabajos, con un nivel de utilidad dado. Otras veces también llamado, precio sombra.

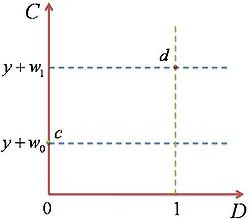
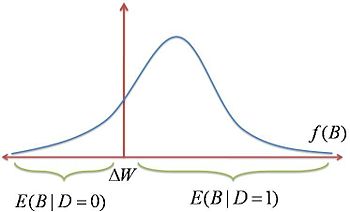
Figura 1. Relación entre las amenidades y el consumo.

Solo para el gráfico definimos y como el ingreso exógeno de cada trabajador y suponemos que éste es fijo a través del tiempo. Las posiciones básicas son como las que se muestran en la Figura 1, donde el punto $(w 0,0)$ representado por $c$ es el ingreso y renta de trabajar en un lugar que presenta amenidades, mientras que el punto $(w 1,1)$ representado por $d$ es el ingreso y renta de trabajar en un lugar con desamenidades, es decir, tanto $c$ como $d$ son las oportunidades de consumo. Si llamamos a $C 0$ el consumo para un trabajo de tipo 0, entonces $C 0 = y + w 0$ (cuando $D = 0$ ). Análogamente, el consumo de un trabajo de tipo 1 seria: $C 1 = y + w 1$ (cuando $D = 1$ ).

Entonces la igualación de diferencias del mercado puede ser expresado de la siguiente forma:
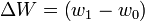
$\Delta W = \left( w_ 1 - w_ 0 \right)$
Lo que significa que el trabajo que cumple con $D = 1$ ofrece $Δ W$ unidades adicionales de ingreso de mercado para compensar las malas condiciones laborales ofrecidas. Y a esto es lo que definimos como el mercado implícito de la amenidad en cuestión.

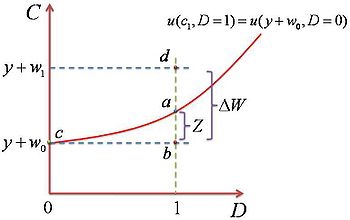
Entonces, un trabajador elige un trabajo tal que se maximice su utilidad. Elegiría $D = 1$ si $u (Δ W + C 0,1)$ . Por otro lado, elegiría $D = 0$ si $u (Δ W + C 0,1) < u (C 0,0)$ . Obviamente, el trabajador seria indiferente entre los 2 tipos de trabajos si las utilidades son las mismas. Ahora volvemos a trazar un nuevo plano $(w, D)$ como el anterior, pero para analizar el umbral de decisión del consumidor. Si $Δ W$ es mayor que la curva de indiferencia, como un punto d, esto implica que D=1 es elegido. Por consecuencia de la idea anterior, si $Δ W$ es tan pequeño que es menor que la curva de indiferencia, entonces la elección es D=0, como un punto b. Dado que $Δ W$ representa la distancia vertical entre la elección de un $D = 0$ y un $D = 1$ , es decir, entre d y b, como se observa en la Figura 2.

Figura 2 .Relación entre las amenidades y el consumo, incluyendo la curva de indiferencia.

Un trabajador ecualiza con $Z$ unidades de consumo adicional para ser compensado al elegir $D = 1$ sobre $D = 0$ . Siendo $Z$ , gráficamente, la distancia vertical entre la decisión final y la curva de indiferencia. La curva de indiferencia está definida donde la utilidad de consumir con un trabajo de tipo 1 es igual a la utilidad de consumir en un trabajo de tipo 0.

Entonces, si $Z > Δ W$ , el trabajo no ofrece compensación suficiente como para que el consumidor de puestos de trabajo, prefiera una ubicación con desamenidades. Finalmente, la regla de decisión del consumidor está descrita como sigue: El trabajador elegirá $D = 1$ si y solo si $Δ W > Z$ , mientras que elegirá $D = 0$ si y solo si $Δ W < Z$ . Resumiendo,

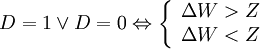
$D=1\vee D=0\Leftrightarrow \left\{ \begin{array}{c} \Delta W>Z \\ \Delta W<Z \end{array} \right.$

Oferta de Mercado

Ergo, la oferta de trabajo es la sumatoria de todas las aplicaciones hechas en todos los tipos de trabajos, para un salario relativo dado. Esta función se encuentra a través de la variación relativa de los salarios, los cuales son determinados a través del comportamiento racional de los trabajadores conducido por la regla de decisión de este. Cada trabajador elige el tipo de trabajo que maximice su utilidad dados los salarios $w 0$ y $w 1$ .

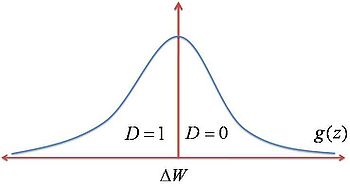
Dado el tamaños de la fuerza laboral que elige entre $D = 0$ y $D = 1$ , la condición de la oferta de mercado relativa es caracterizada por la suma de todos los trabajadores que cumplen $Δ W > Z$ y para quienes se cumple $Δ W < Z$ . Dado que $Δ W$ es el mismo para todos los trabajadores, tenemos que $Z$ es la variable de decisión personal de cada trabajador, la cual depende de las circunstancias y de las preferencias inherentes de cada persona. Finalmente, suponiendo una distribución normal de las decisiones, podemos saber la proporción de trabajadores que toma una elección específica, calculando el área bajo la curva de la función de densidad de probabilidad. Obsérvese la Figura 3.

Figura 3.

Donde $g (z)$ es la función de densidad de probabilidad y por ende, $G (z)$ es la función de densidad acumulada. Luego, a modo de ejemplo, la proporción de trabajadores que elige $D = 1$ estaría determinado por:
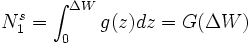
$N_{1}^{s}=\int\nolimits_{0}^{\Delta W}g(z)dz=G(\Delta W)$
Inversamente, la proporción de trabajadores que eligen un tipo de trabajo $D = 0$ es:
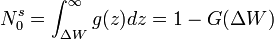
$N_{0} ^{s} = \int \nolimits_ {\Delta W} ^{\infty} g(z) d z = 1 - G ( \Delta W )$
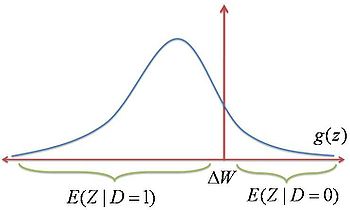
Un aumento del $Δ W$ se vería como un movimiento hacia la derecha del umbral que divide la distribución, como se observa en la Figura 4.

Figura 4.

Recordando, el área, por ejemplo donde se elige $D = 1$ , seria igual a la esperanza condicional de que se obtenga un $Z$ , dado un $D = 1$ .

Elección de la Firma

Para este caso, la firma debe elegir entre el tipo de trabajo que existe en el mercado y este tipo de trabajo depende de la tecnología, la cual determina el tipo de precio ofrecido en cada trabajo. La decisión óptima, entonces, depende de la comparación de los precios de la oferta con el salario de mercado y los costos.

Por ejemplo, la empresa puede gastar recursos en mejorar el ambiente laboral, pero solo dentro de los límites de la tecnología. El costo de hacer esto es comparado con el ahorro de costos laborales disponibles, siempre suponiendo que $w 0 < w 1$ . Así, si el ahorro de costos laborales excede el costo de mejorar, la estrategia óptima es ofrecer el tipo de trabajo $D = 0$ . Mientras que si los costos de mejorar exceden el ahorro de salarios, la firma elegiría ofrecer un tipo de trabajo $D = 1$ en el mercado.

Tenemos, entonces, una función de producción conjunta, $F (x, D, T) = 0$ donde $x$ es el commoditie producido, siendo tanto $x$ como $D$ outpus, y solamente T un input, que es el trabajo aplicado a la producción. Debemos suponer que existen muchas combinaciones de $(x, D)$ tal que la firma puede disponer de recursos como, e.g. disminuir $D$ .

Por Rosen (1974) tenemos que la curva de posibilidades de producción es creciente en $D$ y la pendiente de la curva, será claramente el costo marginal de los cambios en $D$ en términos de $x$ .

Por lo tanto, comparando los costos marginales con las oportunidades de salario se define la elección óptima entre $D = 0$ y $D = 1$ . Construimos los niveles de producción de las firmas para los distintos tipos de trabajo como:

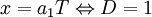
$x = a_1T \Leftrightarrow D = 1$

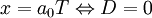
$x = a_0T \Leftrightarrow D = 0$

Donde $a 1$ y $a 0$ son simples parámetros asignados por los puestos de trabajos sin y con amenidades respectivamente, ya que suponemos que la tecnología es lineal. Definimos B como el costo marginal relevante por trabajador de producir en un lugar de trabajo agradable con un producto x conocido (Rosen, 1987).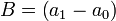
$B = \left( a_1 - a_0 \right)$
Suponemos que $B > 0$ incorpora la idea de que $D = 1$ es productivo, en el sentido de que la eficiencia en el trabajo en la producción de es mayor cuando los recursos no son usados en mejorar el entorno laboral, por lo que la firma elige la alternativa menos costosa.

Para el caso de la firma, finalmente, la regla de decisión es:

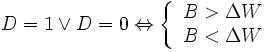
$D=1\vee D=0\Leftrightarrow \left\{ \begin{array}{c} B>\Delta W \\ B<\Delta W \end{array} \right.$

En palabras, si $B$ excede a $Δ W$ el costo conocido de mejorar el ambiente laboral excede el incremento en los costos laborales de proveer un trabajo mejor, entonces, por ejemplo, $D = 1$ es la mejor opción.

Demanda de Mercado

Aquí el análisis es símil a lo revisado anteriormente. La demanda de mercado en cada tipo de trabajo esta en función de las tasas de salarios relativos, condiciones de demanda del producto, etc. Esta demanda de mercado se encuentra a través de la agregación de todas las decisiones de los empleadores. Suponemos tamaño de la firma dado.

Figura 5.

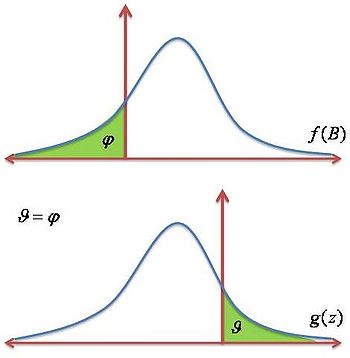
Decimos que $B$ está distribuido a través de las firmas por medio de la función de densidad $f (B)$ y una acumulada $F (B)$ . Entonces $F (B)$ es la fracción de trabajo potencial en el mercado para la cual la tecnología de la firma es $B$ o menor. Como la firma elige de acuerdo a la ecuación de arriba, la fracción de trabajo tipo $D = 1$ ofrecido en el mercado debe ser la suma de todas las firmas donde se cumple que $B > Δ W$ . Específicamente,

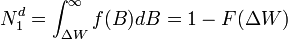
$N_{1}^{d}=\int\nolimits_{\Delta W}^{\infty }f(B)dB=1-F(\Delta W)$

Por otro lado, la fracción de la firma que ofrecerá trabajo de tipo $D = 0$ es la suma de todas las firmas donde se cumple que $B < Δ W$ .

Gráficamente en la Figura 5 se observa, asumiendo normalidad, que la proporción de firmas que elige $D = 1$ se encuentra en el lado derecho del umbral $Δ W$ .

Equilibrio en los Mercados

Definimos el equilibrio de mercado como la igualdad entre la demanda y la oferta para los trabajadores en cada tipo de trabajo, esto dado por:

El nivel de salarios $(w 1, w 2)$ se deba ajustar tal que el número de trabajadores buscando trabajo sea igual a los puestos ofrecidos.

La demanda relativa de trabajadores en $D = 0$ es creciente en $Δ W$ . La demanda relativa de trabajadores en D=1 es decreciente en $Δ W$ .

En consecuencia, las firmas y los trabajadores son sistemáticamente ajustados. En otras palabras, los trabajadores encuentran, en $D = 1$ , trabajos que tienen menos “males” y las firmas ofrecen empleo $D = 1$ teniendo mayores costos de mejorar las áreas de trabajo.

Gráficamente se puede entender como que el área de trabajadores que están dispuestos a trabajar en $D = 1$ (densidad acumulada) es igual a la cantidad de empleadores que ofrecen un puesto de trabajo de tipo $D = 1$ . En la Figura 6 se ve como deben ser equivalentes ambas áreas bajo la curva de densidad de probabilidad.

Figura 6.

Conclusión

El estudio de las amenidades, mercados implícitos y ecualización de diferencias salariales, en la decisión tanto de las firmas como de los trabajadores, ha entregado precisión y técnica al repertorio de la economía laboral. Aunque el padre de este método no esté definido claramente, hoy se cuenta con aportes importantes teóricos y empíricos, que permiten adecuar el método a distintos contextos económicos. Tras revisar el modelo urbano de salarios hedónicos se concluye que pensar que solo los precios determinan la decisiones de los agentes al momento de contratar u ofrecer trabajo, es incorrecto, sino que depende del salario, la renta, la influencia de la amenidad en la producción y, finalmente, de las preferencias inherentes en cada consumidor.

Referencias

Court. A T. “Hedonic Process Indexes With Automobile Example.” The dynamics of automobile demand, New York: general Motors. 1939.

Griliches, Z. “Hedonic Prices Indexes For Automobiles An Econometric Analysis Of Quality Change.” The Price Statistics of Federal Government, hearing before the Joint Economic Committee of the U.S Congress, 173-176. Pt. 1, 87 th Cong,. 1st sess. 1961.

Hass, G.C. “A statistical analysis of farm sales in blue earth country, Minnesota, as a basis for farm land appraisal.” Master’s thesis, University of Minnesota. 1922.

Hoehn, J; M. Berger y G. Blomquist. "A Hedonic Model of Interregional Wages, rents and Amenity Values." Journal of Regional Sciences, Vol 27, No 4, 1988.

Roback, Jennifer. “Wages, Rents, and the Quality of Life.” The Journal of Political Economy, Vol. 90, No. 6, 1982.

Rosen, Sherwin. “Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition.” The Journal of Political Economy, Vol. 82, No. 1, 1974.

Rosen, Sherwin. “Handbook of Labor Economics”. Vol. 1, Cap. 12, North Holland, Amsterdam. 1987.

Taylor, L. “The Hedonic Method”. En P. Champ., K: Boyle y T. Brown, A primer on non-market valuation, London: Kluwer Academic Publishing. 2003.

Vasquez, F.; Cerda, A; Orrego, S. "Valoración Económica del Medio Ambiente. Fundamentos Economicos, econometricos y aplicaciones" 1 Ed. Thompson 2006.

Wallace, H. “Comparative Farmland Values In Iowa.” Journal of Land and Public Utility Economics 2, 385-392. 1926.

Wuagh, F. “Quality Factors Influencing Vegetable Prices.” Journal of Farm Economics 10. 185-196. 1928.

Obtenido de "Salario Hed%C3%B3nico"

Categorías: Trabajo | Terminología económica