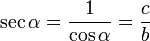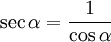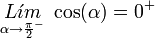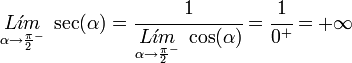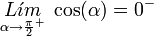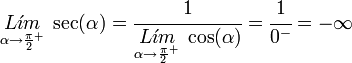Secante (Trigonometría)

Secante (Trigonometría)

Secante (Trigonometría)

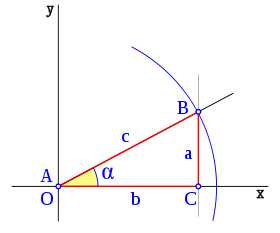
Trigono b00.svg

La Secante, (abreviado como sec), es la razón trigonométrica recíproca del coseno, o también su inverso multiplicativo:

\sec \alpha = \frac{1}{\cos \alpha} = \frac{c}{b}

Contenido

Representación gráfica

FunTriR020.svg

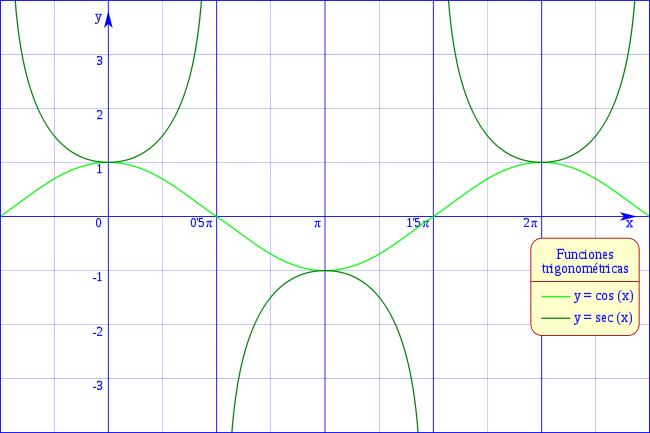
Coseno y secante de un ángulo

Partiendo de la definición de secante como la inversa del coseno:

\sec \alpha = \frac{1}{\cos \alpha}
FunTriR030.svg

Conociendo la función coseno, podemos ver que para los valores en los que el coseno vale cero, la secante se hace infinito, si la función coseno tiende a cero desde valores positivos la secante tiende a más infinito:

\underset {\alpha \to {\frac{\pi}{2}}^-} {L \acute{\imath}m} \; \cos(\alpha) = 0^+
\underset {\alpha \to {\frac{\pi}{2}}^-} {L \acute{\imath}m} \; \sec (\alpha) = \cfrac {1} {\underset {\alpha \to {\frac{\pi}{2}}^-} {L \acute{\imath}m} \; \cos(\alpha)} = \cfrac{1}{0^+} = + \infty

mientras que cuando el coseno tiende a cero desde valores negativos la secante tiende a menos infinito.

\underset {\alpha \to {\frac{\pi}{2}}^+} {L \acute{\imath}m} \; \cos(\alpha) = 0^-
\underset {\alpha \to {\frac{\pi}{2}}^+} {L \acute{\imath}m} \; \sec (\alpha) = \cfrac {1} {\underset {\alpha \to {\frac{\pi}{2}}^+} {L \acute{\imath}m} \; \cos(\alpha)} = \cfrac{1}{0^-} = - \infty

Cuando el coseno del ángulo vale uno, su secante también vale uno, como se puede ver en la gráfica.

Véase también

Referencias

Bibliografía

  1. Cobo Mérida, Purificación (9 de 2008). Trigonometría, 4 ESO (en español). Materiales Didacticos Bemal. ISBN 978-84-612-6049-2.
  2. Cortés Espinosa de los Monteros, Nuria (2 de 2008). Actividades para unidad didáctica sobre trigonometría (en español). Ediciones Didacticas y Pedagogicas S.L.. ISBN 978-84-936336-3-9. «1 CD-ROM»
  3. Merlini Navarro, Irene (2 de 2008). Trigonometría plana : tu material didáctico, 1 edición (en español), Vision Libros. ISBN 978-84-9821-279-2. «1 CD-ROM»

Enlaces externos

Obtenido de "Secante (Trigonometr%C3%ADa)"

Wikimedia foundation. 2010.

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

  • Secante (trigonometría) — La Secante, (abreviado como sec), es la razón trigonométrica inversa del coseno, o también su inverso multiplicativo: Contenido 1 Explicación …   Wikipedia Español

  • Trigonometría — La trigonometría es una rama de la matemática, cuyo significado etimológico es la medición de los triángulos . Deriva de los términos griegos τριγωνο trigōno triángulo y μετρον metron medida.[1] En términos generales, la trigonometría es el… …   Wikipedia Español

  • Secante — I (Derivado de secar.) ► adjetivo/ sustantivo 1 Que seca o elimina la humedad o el agua. ► adjetivo/ sustantivo masculino 2 Se aplica al papel que es esponjoso y que sirve para secar la tinta de la escritura. ► sustantivo 3 DEPORTES Jugador que,… …   Enciclopedia Universal

  • Trigonometría — (Del gr. trigonos, trígono + metron, medida.) ► sustantivo femenino 1 MATEMÁTICAS Parte de las matemáticas dedicada al estudio de las relaciones entre las amplitudes de los ángulos y las longitudes de los segmentos que sus lados determinan en las …   Enciclopedia Universal

  • secante — se·càn·te p.pres., agg., s.f. 1. p.pres., agg. → secare 2. s.f. TS geom. → retta secante 3. s.f. TS mat. in trigonometria, funzione di un angolo pari all inverso del suo coseno (simb. 2sec) …   Dizionario italiano

  • Recta secante — Para la razón trigonométrica recíproca del coseno, véase secante (trigonometría). Recta secante que corta una circunferencia …   Wikipedia Español

  • trigonométrie — [ trigɔnɔmetri ] n. f. • 1613; lat. sc. trigonometria (1595); cf. trigone et métrie 1 ♦ Sc. Branche des mathématiques dont le principal objet est l application du calcul à la détermination des éléments des triangles, au moyen des fonctions… …   Encyclopédie Universelle

  • Función trigonométrica — En matemáticas, Las funciones trigonométricas son las funciones que se definen a fin de extender la definición de las razones trigonométricas a todos los números reales. Las funciones trigonométricas son de gran importancia en física, astronomía …   Wikipedia Español

  • Prostaféresis — Saltar a navegación, búsqueda La prostaféresis o prostafairesis es un algoritmo utilizado a finales del siglo XVI y principios del XVII para aproximar la multiplicación y división de números mediante identidades trigonométricas. Durante los 25… …   Wikipedia Español

  • cosecante — ► sustantivo femenino GEOMETRÍA Secante del complemento de un ángulo o de un arco. * * * cosecante f. Geom. Secante del complemento del ángulo o el arco de que se trata. ⇒ *Trigonometría. * * * cosecante. f. Mat. Inversa del seno de un ángulo o… …   Enciclopedia Universal

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”