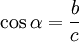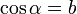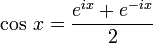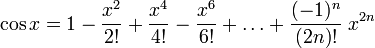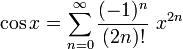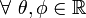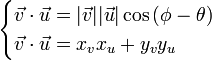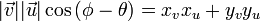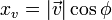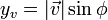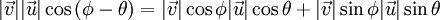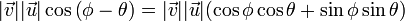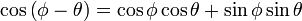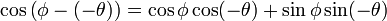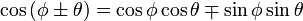Coseno

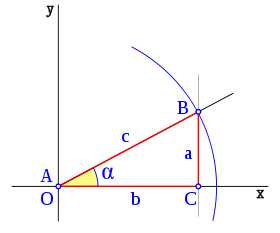
En trigonometría el coseno (abreviado cos) de un ángulo en un triángulo rectángulo se define como la razón entre el cateto adyacente y la hipotenusa:

$\cos\alpha = \frac{b}{c}$

O también como la abscisa correspondiente a un punto que pertenece a una circunferencia unitaria centrada en el origen (c = 1).

$\cos\alpha = b \,$

En matemáticas el coseno es la función obtenida al hacer variar la razón mencionada, siendo una de las funciones trascendentes.

También se puede definir mediante exponenciales de la forma:

${\rm cos\ }x=\frac{e^{ix} + e^{-ix} }{2}$

Donde i es la unidad imaginaria.

Contenido

1 El coseno como serie de Taylor
2 Representación gráfica
3 Coseno de una suma o resta de ángulos
4 Coseno de un ángulo doble
5 Coseno del ángulo medio
6 Transformación de una suma de cosenos en producto
7 Derivada del Coseno
8 Generalizaciones del coseno
9 Véase también

El coseno como serie de Taylor

Su expansión en Serie de Taylor en torno a x=0 es:

$\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots + \frac{(-1)^n}{(2n)!} \; x^{2n}$

$\cos x = \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!} \; x^{2n}$

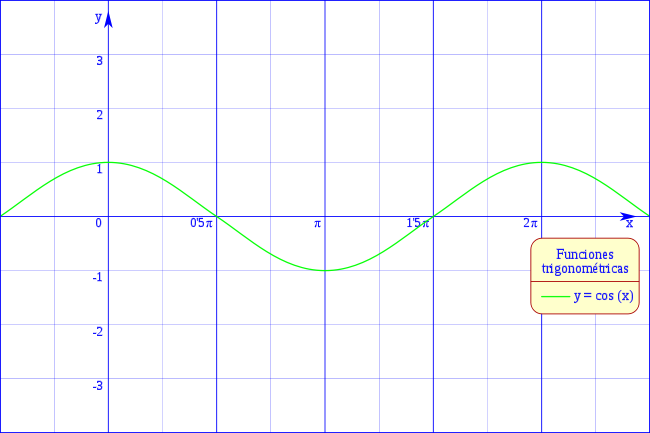
Representación gráfica

Coseno de una suma o resta de ángulos

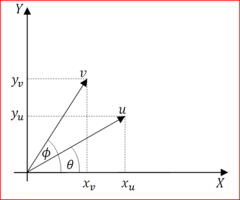
Coseno de la diferencia de dos ángulos

Esta identidad trigonométrica se muestra a partir del producto escalar de dos vectores.

$\forall\ \theta,\phi\in\mathbb{R}$

Utilizando las dos definiciones de producto escalar se obtiene:

$\begin{cases} \vec{v}\cdot\vec{u}=|\vec{v}||\vec{u}|\cos\left(\phi - \theta \right)\\ \vec{v}\cdot\vec{u}=x_vx_u+y_vy_u\\ \end{cases}$

Por igualación se define que

$|\vec{v}||\vec{u}|\cos\left(\phi - \theta\right)=x_vx_u+y_vy_u$

Las componentes de los vectores se pueden reemplazar como la proyección de su módulo sobre los ejes, es decir

$x_v=|\vec{v}|\cos\phi$

$y_v=|\vec{v}|\sin\phi$

Reemplazando esta propiedad en ambos vectores nos queda

$|\vec{v}||\vec{u}|\cos\left(\phi -\theta\right)=|\vec{v}|\cos\phi|\vec{u}|\cos\theta+|\vec{v}|\sin\phi|\vec{u}|\sin\theta$

Extrayendo como factor común los módulos de los vectores en el segundo miembro

$|\vec{v}||\vec{u}|\cos \left(\phi -\theta\right)=|\vec{v}||\vec{u}|(\cos\phi\cos\theta+\sin\phi\sin\theta)$

Simplificando nos queda la identidad trigonométrica

$\cos\left(\phi-\theta\right)=\cos\phi\cos\theta+\sin\phi\sin\theta$

Coseno de la suma de dos ángulos

Si hacemos

$\cos\left(\phi-(-\theta\right))=\cos\phi\cos(-\theta)+\sin\phi\sin(-\theta)$

obtenemos la resta. Como el coseno es par, el signo no importa y como el seno es impar, el signo sale

$\cos\left(\phi+\theta\right)=\cos\phi\cos\theta-\sin\phi\sin\theta$

Forma resumida

$\cos\left(\phi\pm\theta\right)=\cos\phi\cos\theta\mp\sin\phi\sin\theta$

Coseno de un ángulo doble

Tenemos que

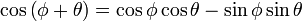
$\cos\left(\phi +\theta\right)=\cos\phi\cos\theta-\sin\phi\sin\theta$

Hagamos 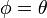$\phi=\theta\,$ Entonces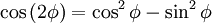

$\cos\left(2\phi\right)=\cos^2\phi-\sin^2\phi$

Coseno del ángulo medio

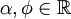
Nótese que con un simple manejo algebraico podemos obtener la fórmula del coseno del ángulo medio. Sea $\alpha, \phi \in \mathbb{R}$

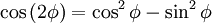
Como $\cos\left(2\phi\right)=\cos^2\phi-\sin^2\phi$

la podemos escribir como

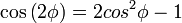
$\cos\left(2\phi\right)=2cos^2\phi-1$

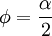
Sea $\phi=\frac{\alpha}{2}$

Entonces obtenemos

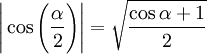
$\Bigg|\cos\Bigg(\frac{\alpha}{2}\Bigg)\Bigg|=\sqrt{\frac{\cos\alpha+1}{2}}$

y analizando los signos de la expresión para cada cuadrante, concluimos que:

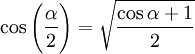
$\cos\Bigg(\frac{\alpha}{2}\Bigg)=\sqrt{\frac{\cos\alpha+1}{2}}$

Transformación de una suma de cosenos en producto

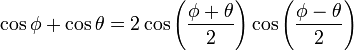
$\cos\phi+\cos\theta=2\cos\Bigg(\frac{\phi+\theta}{2}\Bigg)\cos\Bigg(\frac{\phi-\theta}{2}\Bigg)$

Demostración

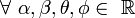
Sabiendo que $\forall\ \alpha,\beta,\theta,\phi \in\ \mathbb{R}$

Entonces

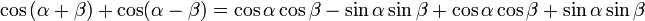
$\cos\left(\alpha+\beta\right)+\cos(\alpha-\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta+\cos\alpha\cos\beta+\sin\alpha\sin\beta$

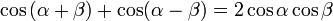
$\cos\left(\alpha+\beta\right)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta$

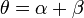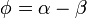
Hagamos $\theta=\alpha+\beta\,$ y $\phi=\alpha-\beta\,$

Entonces, resolviendo el sistema se tiene que

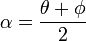
$\alpha=\frac{\theta+\phi}{2}$

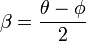
$\beta=\frac{\theta-\phi}{2}$

Reemplazando se obtiene

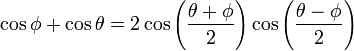
$\cos\phi+\cos\theta=2\cos\Bigg(\frac{\theta+\phi}{2}\Bigg)\cos\Bigg(\frac{\theta-\phi}{2}\Bigg)$

Análogamente se demuestra para

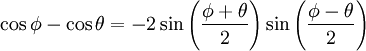
$\cos\phi-\cos\theta=-2\sin\Bigg(\frac{\phi+\theta}{2}\Bigg)\sin\Bigg(\frac{\phi-\theta}{2}\Bigg)$

Derivada del Coseno

Según la definición de derivada:

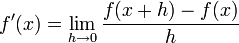
$f'(x)=\lim_{h\rightarrow0} \frac{f(x + h) - f(x)}{h}$

lo que es

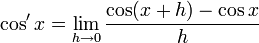
$\cos'x=\lim_{h\rightarrow0} \frac{\cos(x + h)-\cos x}{h}$

Entonces, usando las fórmulas anteriormente señaladas, se tiene que

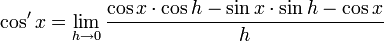
$\cos'x=\lim_{h\rightarrow0} \frac{\cos x\cdot \cos h-\sin x\cdot\sin h-\cos x}{h}$

Factorizando

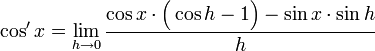
$\cos'x=\lim_{h\rightarrow0} \frac{\cos x\cdot\Big(\cos h-1\Big)-\sin x\cdot\sin h}{h}$

Separando, sabiendo que todas las funciones son continuas, tenemos

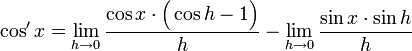
$\cos'x=\lim_{h\rightarrow0} \frac{\cos x\cdot\Big(\cos h -1\Big)}{h}- \lim_{h\rightarrow0} \frac{\sin x\cdot\sin h}{h}$

Sabiendo que 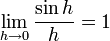$\lim_{h\rightarrow0} \frac{\sin h}{h}=1$ y que el primer límite queda determinado utilizando las relaciones de suma de senos junto con el límite recién escrito, se obtiene que el primer término queda determinado y da 0, entonces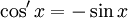

$\cos'x=-\sin x\,$

Generalizaciones del coseno

Véase también

Obtenido de "Coseno"

Categoría: Funciones trigonométricas

Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

coseno — sustantivo masculino 1. Área: matemáticas Seno del complemento de un ángulo o de un arco: El coseno y la secante dependen de la abscisa del extremo del arco … Diccionario Salamanca de la Lengua Española
coseno — m. Mat. Seno del complemento de un ángulo o de un arco. coseno verso. m. Mat. Seno verso del complemento de un ángulo o de un arco … Diccionario de la lengua española
Coseno — ► sustantivo masculino GEOMETRÍA Seno del complemento de un ángulo o de un arco. * * * coseno m. Geom. Con respecto a un ángulo o al arco correspondiente, relación entre el cateto contiguo y la hipotenusa de cualquier triángulo rectángulo formado … Enciclopedia Universal
coseno — {{＃}}{{LM C10701}}{{〓}} {{［}}coseno{{］}} ‹co·se·no› {{《}}▍ s.m.{{》}} {{♂}}En trigonometría,{{♀}} razón entre el cateto contiguo de un ángulo y la hipotenusa: • El coseno no depende de la longitud de los lados del triángulo.{{○}} … Diccionario de uso del español actual con sinónimos y antónimos
Coseno hiperbólico — Saltar a navegación, búsqueda Gráfica de la función , sobre los reales. El coseno hiperbólico de un número real … Wikipedia Español
coseno — m Relaciуn entre el lado adyacente a un бngulo dado y su hipotenusa … Diccionario de Construcción y Arquitectur
coseno — co·sé·no s.m. 1. TS mat. in una circonferenza unitaria con il centro nell origine di un sistema di coordinate cartesiane, funzione trigonometrica che fa corrispondere al valore di un angolo, individuato dall asse delle ascisse e da un raggio, l… … Dizionario italiano
coseno — {{hw}}{{coseno}}{{/hw}}s. m. In trigonometria, misura con segno della proiezione ortogonale, su un lato dell angolo, d un segmento unitario giacente sull altro lato … Enciclopedia di italiano
coseno — s m (Mat) Con respecto a un ángulo, función trigonométrica definida por la división del cateto adyacente entre la hipotenusa de cualquier triángulo rectángulo formado sobre ese ángulo; con respecto a un arco, esta misma función considerando el… … Español en México
coseno — pl.m. coseni … Dizionario dei sinonimi e contrari

Los diccionarios y las enciclopedias sobre el Académico

Coseno

Coseno

Contenido

El coseno como serie de Taylor

Representación gráfica