Tabla hash

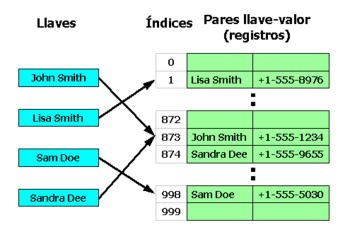
Una tabla hash o mapa hash es una estructura de datos que asocia llaves o claves con valores. La operación principal que soporta de manera eficiente es la búsqueda: permite el acceso a los elementos (teléfono y dirección, por ejemplo) almacenados a partir de una clave generada (usando el nombre o número de cuenta, por ejemplo). Funciona transformando la clave con una función hash en un hash, un número que la tabla hash utiliza para localizar el valor deseado.

Ejemplo de tabla hash.

Las tablas hash se suelen implementar sobre vectores de una dimensión, aunque se pueden hacer implementaciones multi-dimensionales basadas en varias claves. Como en el caso de los arrays, las tablas hash proveen tiempo constante de búsqueda promedio O(1),^[1] sin importar el número de elementos en la tabla. Sin embargo, en casos particularmente malos el tiempo de búsqueda puede llegar a O(n), es decir, en función del número de elementos.

Comparada con otras estructuras de arrays asociadas, las tablas hash son más útiles cuando se almacenan grandes cantidades de información.

Las tablas hash almacenan la información en posiciones pseudo-aleatorias, así que el acceso ordenado a su contenido es bastante lento. Otras estructuras como árboles binarios auto-balanceables son más rápidos en promedio (tiempo de búsqueda O(log n)) pero la información está ordenada en todo momento.

Funcionamiento

Las operaciones básicas implementadas en las tablas hash son:

inserción(llave, valor)

búsqueda(llave) que devuelve valor

La mayoría de las implementaciones también incluyen borrar(llave). También se pueden ofrecer funciones como iteración en la tabla, crecimiento y vaciado. Algunas tablas hash permiten almacenar múltiples valores bajo la misma clave.

Para usar una tabla hash se necesita:

• Una estructura de acceso directo (normalmente un array).
• Una estructura de datos con una clave
• Una función resumen (hash) cuyo dominio sea el espacio de claves y su imagen (o rango) los números naturales.

Inserción

1. Para almacenar un elemento en la tabla hash se ha de convertir su clave a un número. Esto se consigue aplicando la función resumen (hash) a la clave del elemento.
2. El resultado de la función resumen ha de mapearse al espacio de direcciones del arreglo que se emplea como soporte, lo cual se consigue con la función módulo. Tras este paso se obtiene un índice válido para la tabla.
3. El elemento se almacena en la posición de la tabla obtenido en el paso anterior.
   1. Si en la posición de la tabla ya había otro elemento, se ha producido una colisión. Este problema se puede solucionar asociando una lista a cada posición de la tabla, aplicando otra función o buscando el siguiente elemento libre. Estas posibilidades han de considerarse a la hora de recuperar los datos.

Búsqueda

1. Para recuperar los datos, es necesario únicamente conocer la clave del elemento, a la cual se le aplica la función resumen.
2. El valor obtenido se mapea al espacio de direcciones de la tabla.
3. Si el elemento existente en la posición indicada en el paso anterior tiene la misma clave que la empleada en la búsqueda, entonces es el deseado. Si la clave es distinta, se ha de buscar el elemento según la técnica empleada para resolver el problema de las colisiones al almacenar el elemento.

Prácticas recomendadas para las funciones hash

Una buena función hash es esencial para el buen rendimiento de una tabla hash. Las colisiones son generalmente resueltas por algún tipo de búsqueda lineal, así que si la función tiende a generar valores similares, las búsquedas resultantes se vuelven lentas.

En una función hash ideal, el cambio de un simple bit en la llave (incluyendo el hacer la llave más larga o más corta) debería cambiar la mitad de los bits del hash, y este cambio debería ser independiente de los cambios provocados por otros bits de la llave. Como una función hash puede ser difícil de diseñar, o computacionalmente cara de ejecución, se han invertido muchos esfuerzos en el desarrollo de estrategias para la resolución de colisiones que mitiguen el mal rendimiento del hasheo. Sin embargo, ninguna de estas estrategias es tan efectiva como el desarrollo de una buena función hash de principio.

Es deseable utilizar la misma función hash para arrays de cualquier tamaño concebible. Para esto, el índice de su ubicación en el array de la tabla hash se calcula generalmente en dos pasos:

1. Un valor hash genérico es calculado, llenando un entero natural de máquina.

2. Este valor es reducido a un índice válido en el vector encontrando su módulo con respecto al tamaño del array.

El tamaño del vector de las tablas hash es con frecuencia un número primo. Esto se hace con el objetivo de evitar la tendencia de que los hash de enteros grandes tengan divisores comunes con el tamaño de la tabla hash, lo que provocaría colisiones tras el cálculo del módulo. Sin embargo, el uso de una tabla de tamaño primo no es un sustituto a una buena función hash.

Un problema bastante común que ocurre con las funciones hash es el aglomeramiento. El aglomeramiento ocurre cuando la estructura de la función hash provoca que llaves usadas comúnmente tiendan a caer muy cerca unas de otras o incluso consecutivamente en la tabla hash. Esto puede degradar el rendimiento de manera significativa, cuando la tabla se llena usando ciertas estrategias de resolución de colisiones, como el sondeo lineal.

Cuando se depura el manejo de las colisiones en una tabla hash, suele ser útil usar una función hash que devuelva siempre un valor constante, como 1, que cause colisión en cada inserción.

Funciones Hash más usadas:

1. Hash de División:

Dado un diccionario D, se fija un número m >= |D| (m mayor o igual al tamaño del diccionario) y que sea primo no cercano a potencia de 2 o de 10. Siendo k la clave a buscar y h(k) la función hash, se tiene h(k)=k%m (Resto de la división k/m).

2. Hash de Multiplicación

Si por alguna razón, se necesita una tabla hash con tantos elementos o punteros como una potencia de 2 o de 10, será mejor usar una función hash de multiplicación, independiente del tamaño de la tabla. Se escoge un tamaño de tabla m >= |D| (m mayor o igual al tamaño del diccionario) y un cierto número irracional φ (normalmente se usa 1+5^(1/2)/2 o 1-5^(1/2)/2). De este modo se define h(k)= Suelo(m*Parte fraccionaria(k*φ))

Resolución de colisiones

Si dos llaves generan un hash apuntando al mismo índice, los registros correspondientes no pueden ser almacenados en la misma posición. En estos casos, cuando una casilla ya está ocupada, debemos encontrar otra ubicación donde almacenar el nuevo registro, y hacerlo de tal manera que podamos encontrarlo cuando se requiera.

Para dar una idea de la importancia de una buena estrategia de resolución de colisiones, considerese el siguiente resultado, derivado de la paradoja de las fechas de nacimiento. Aun cuando supongamos que el resultado de nuestra función hash genera índices aleatorios distribuidos uniformemente en todo el vector, e incluso para vectores de 1 millón de entradas, hay un 95% de posibilidades de que al menos una colisión ocurra antes de alcanzar los 2.500 registros.

Hay varias técnicas de resolución de colisiones, pero las más populares son encadenamiento y direccionamiento abierto.

Direccionamiento Cerrado o Encadenamiento separado o Hashing abierto

En la técnica más simple de encadenamiento, cada casilla en el array referencia una lista de los registros insertados que colisionan en la misma casilla. La inserción consiste en encontrar la casilla correcta y agregar al final de la lista correspondiente. El borrado consiste en buscar y quitar de la lista.

Ejemplo de encadenamiento.

La técnica de encadenamiento tiene ventajas sobre direccionamiento abierto. Primero el borrado es simple y segundo el crecimiento de la tabla puede ser pospuesto durante mucho más tiempo dado que el rendimiento disminuye mucho más lentamente incluso cuando todas las casillas ya están ocupadas. De hecho, muchas tablas hash encadenadas pueden no requerir crecimiento nunca, dado que la degradación de rendimiento es lineal en la medida que se va llenando la tabla. Por ejemplo, una tabla hash encadenada con dos veces el número de elementos recomendados, será dos veces más lenta en promedio que la misma tabla a su capacidad recomendada.

Las tablas hash encadenadas heredan las desventajas de las listas ligadas. Cuando se almacenan cantidades de información pequeñas, el gasto extra de las listas ligadas puede ser significativo. También los viajes a través de las listas tienen un rendimiento de caché muy pobre.

Otras estructuras de datos pueden ser utilizadas para el encadenamiento en lugar de las listas ligadas. Al usar árboles auto-balanceables, por ejemplo, el tiempo teórico del peor de los casos disminuye de O(n) a O(log n). Sin embargo, dado que se supone que cada lista debe ser pequeña, esta estrategia es normalmente ineficiente a menos que la tabla hash sea diseñada para correr a máxima capacidad o existan índices de colisión particularmente grandes. También se pueden utilizar vectores dinámicos para disminuir el espacio extra requerido y mejorar el rendimiento del caché cuando los registros son pequeños.

Direccionamiento abierto o Hashing cerrado

Las tablas hash de direccionamiento abierto pueden almacenar los registros directamente en el array. Las colisiones se resuelven mediante un sondeo del array, en el que se buscan diferentes localidades del array (secuencia de sondeo) hasta que el registro es encontrado o se llega a una casilla vacía, indicando que no existe esa llave en la tabla.

Ejemplo de direccionamiento abierto.

Las secuencias de sondeo más socorridas incluyen:

sondeo lineal

en el que el intervalo entre cada intento es constante (frecuentemente 1).

sondeo cuadrático

en el que el intervalo entre los intentos aumenta linealmente (por lo que los índices son descritos por una función cuadrática), y

doble hasheo

en el que el intervalo entre intentos es constante para cada registro pero es calculado por otra función hash.

El sondeo lineal ofrece el mejor rendimiento del caché, pero es más sensible al aglomeramiento, en tanto que el doble hasheo tiene pobre rendimiento en el caché pero elimina el problema de aglomeramiento. El sondeo cuadrático se sitúa en medio. El doble hasheo también puede requerir más cálculos que las otras formas de sondeo.

Una influencia crítica en el rendimiento de una tabla hash de direccionamiento abierto es el porcentaje de casillas usadas en el array. Conforme el array se acerca al 100% de su capacidad, el número de saltos requeridos por el sondeo puede aumentar considerablemente. Una vez que se llena la tabla, los algoritmos de sondeo pueden incluso caer en un círculo sin fin. Incluso utilizando buenas funciones hash, el límite aceptable de capacidad es normalmente 80%. Con funciones hash pobremente diseñadas el rendimiento puede degradarse incluso con poca información, al provocar aglomeramiento significativo. No se sabe a ciencia cierta qué provoca que las funciones hash generen aglomeramiento, y es muy fácil escribir una función hash que, sin querer, provoque un nivel muy elevado de aglomeramiento.

Ventajas e inconvenientes de las tablas hash

Una tabla hash tiene como principal ventaja que el acceso a los datos suele ser muy rápido si se cumplen las siguientes condiciones:

• Una razón de ocupación no muy elevada (a partir del 75% de ocupación se producen demasiadas colisiones y la tabla se vuelve ineficiente).
• Una función resumen que distribuya uniformemente las claves. Si la función está mal diseñada, se producirán muchas colisiones.

Los inconvenientes de las tablas hash son:

• Necesidad de ampliar el espacio de la tabla si el volumen de datos almacenados crece. Se trata de una operación costosa.
• Dificultad para recorrer todos los elementos. Se suelen emplear listas para procesar la totalidad de los elementos.
• Desaprovechamiento de la memoria. Si se reserva espacio para todos los posibles elementos, se consume más memoria de la necesaria; se suele resolver reservando espacio únicamente para punteros a los elementos.

Implementación en pseudocódigo

El pseudocódigo que sigue es una implementación de una tabla hash de direccionamiento abierto con sondeo lineal para resolución de colisiones y progresión sencilla, una solución común que funciona correctamente si la función hash es apropiada.

 registro par { llave, valor }
 var vector de pares casilla[0..numcasillas-1]
 
 function buscacasilla(llave) {
     i := hash(llave) módulo de numcasillas
     loop {
         if casilla[i] esta libre or casilla[i].llave = llave
             return i
         i := (i + 1) módulo de numcasillas
     }
 }
 
 function busqueda(llave)
     i := buscacasilla(llave)
     if casilla[i] está ocupada   // llave está en la tabla
         return casilla[i].valor
     else                     // llave no está en la tabla
         return no encontrada   
 
 function asignar(llave, valor) {
     i := buscacasilla(llave)
     if casilla[i] está ocupada
         casilla[i].valor := valor
     else {
         if tabla casi llena {
             hacer tabla más grande (nota 1)
             i := buscacasilla(llave)
         }
         casilla[i].llave := llave
         casilla[i].valor := valor
     }
 }

Nota

1. ↑ La reconstrucción de la tabla requiere la creación de un array más grande y el uso posterior de la función asignar para insertar todos los elementos del viejo array en el nuevo array más grande. Es común aumentar el tamaño del array exponencialmente, por ejemplo duplicando el tamaño del array.

Enlaces externos

Artículos e implementaciones

• Artículo donde se explica la implementación en C y un análisis de costo-beneficio de una tabla hash.

• Ejemplo de implementación de tabla hash en C++.