Teorema de Boucherot

El teorema de Boucherot, ideado por Paul Boucherot, permite la resolución del cálculo total de potencias en circuitos de corriente alterna. De acuerdo con este teorema, las potencias activa y reactiva totales en un circuito, vienen dadas por la suma de las potencias activa y reactiva, respectivamente, de cada una de sus cargas. De forma analítica:

Seguidamente se demostrarán ambas igualdades para un receptor serie y para otro paralelo.

Receptor en serie

Figura 1: Receptor serie, a, y diagrama fasorial, b.

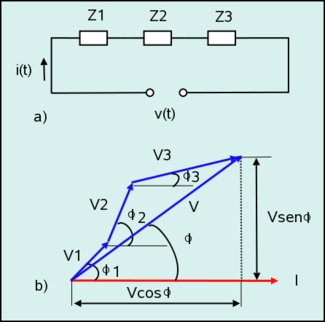
Sea el circuito serie de la figura 1a. Aplicando la ley de Ohm

Tomando la intensidad en el origen de fases (figura 1b),

y sustituyendo

Por otro lado, el valor de puede expresarse como (ver figura 1b):

Comparando ambas igualdades

Finalmente si multiplicamos ambas expresiones por I, se deduce

Receptor en paralelo

Figura 2: Receptor paralelo, a, y diagrama fasorial, b.

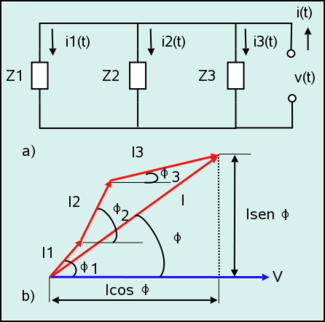
Sea el circuito paralelo y su correspondiente diagrama fasorial, figuras 2a y 2b respectivamente. Las componentes activa y rectiva de la corriente total, I_a e I_r, vienen dadas como suma de las componentes parciales de cada una de la corrientes que circulan por cada rama:

Sustituyendo por sus valores:

Y si estas expresiones se multiplican por V, se obtiene

Que es el mismo resultado que para un receptor serie. En ambos casos, generalizando

que es lo que se deseaba demostrar.

Potencia aparente total

Figura 3: Triángulo de potencias de una instalación con tres receptores, el 1 y el 2 inductivos y el 3 capacitivo.

Los dos puntos anteriores no implican que la potencia aparente total de un sistema se obtenga como suma de las potencias aparentes parciales:

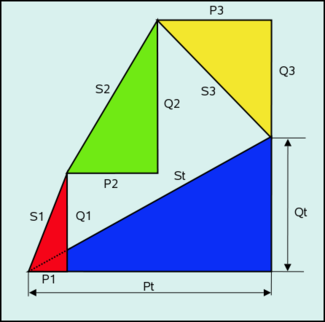
Gráficamente, para efectuar el balance de potencias de una instalación, es necesario obtener el triángulo total de potencias como suma de los triángulos de potencia parciales de cada receptor. Si por ejemplo tuviéramos tres receptores, dos inductivos y uno capacitivo, su triángulo de potencias sería similar al mostrado en la figura 3, donde se deduce que