El teorema de la estadística del spin de la mecánica cuántica establece la relación directa entre el spin de una especie de partícula con la estadística que obedece. Fue demostrado por Fierz y Pauli en 1940, y requiere el formalismo de teoría cuántica de campos.

Relación empírica

El spin es un momento angular intrínseco (no asociado a su movimiento espacial) que posee toda partícula a nivel cuántico. Puede tomar valores enteros o semienteros, en unidades de la constante de Planck .

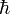La estadística de una especie de partículas determina su comportamiento colectivo. Si pueden redistribuirse libremente en todas las configuraciones posibles del sistema, se denominan bosones. Si por el contrario obedecen el principio de exclusión de Pauli que restringe estas configuraciones, se denominan fermiones.

Estas dos características están en aparencia totalmente descorrelacionadas. Sin embargo es un hecho experimental que todos los bosones poseen spin entero, mientras que los fermiones poseen spin semientero.

Enunciado

El teorema dice:

• Las funciones de onda de un sistema de partículas idénticas con spin entero, conocidas como bosones, (esto es, s = 0, 1, 2,...) son simétricas bajo el intercambio de cualquier par de partículas.

• Las funciones de onda de un sistema de partículas idénticas con spin semientero, conocidas como fermiones, (esto es, s = 1/2, 3/2, 5/2,...) son anti-simétricas bajo el intercambio de cualquier par de partículas.

El teorema implica que los fermiones están sujetos al principio de exclusión de Pauli, mientras que los bosones no lo están. Esto significa que un estado cuántico sólo puede estar ocupado por un fermión, mientras que los bosones no tienen esa restricción. Los protones, neutrones, y electrones son fermiones. Otras partículas, como los fotones, que median en las fuerzas entre partículas, son bosones.

Consecuencias

Hay un par de fenómenos interesantes facilitados por los dos tipos de estadística. La distribución de Bose-Einstein describe los bosones en un condensado Bose-Einstein. Bajo una cierta temperatura, la mayoría de las partículas en un sistema bosónico estará en el estado fundamental (el de más baja energía). De ahí resultan propiedades inusuales como la superfluidez.

La distribución de Fermi-Dirac, que describe el comportamiento de los fermiones, también proporciona interesantes propiedades. Dado que sólo un único fermión puede ocupar un estado cuántico, el nivel fundamental de energía sólo puede ser ocupado por dos fermiones, con sus spins alineados de manera contraria. Así, incluso al cero absoluto de temperatura, el sistema tiene una cierta energía diferente de cero. Como resultado, un sistema fermiónico ejerce presión externa. Aun a temperaturas diferentes de cero, dicha presión existe. Esta presión es la responsable de que ciertas estrellas masivas no puedan colapsar debido a la gravedad (ver enana blanca, estrella de neutrones, y agujero negro).

Referencias

• W. Pauli, The Connection Between Spin and Statistics, Phys. Rev. 58, 716-722(1940). (abstract)
• Paul O'Hara, Rotational Invariance and the Spin-Statistics Theorem, Foun. Phys. 33, 1349-1368(2003).