Teorema del aumento de velocidad lineal

Teorema del aumento de velocidad lineal

Teorema del aumento de velocidad lineal

En Teoría de la complejidad computacional, el teorema del aumento de velocidad lineal por máquinas de Turing es el siguiente:

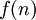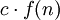Dado c > 0 y cualquier máquina de Turing que resuelve un problema en tiempo f(n)\,, hay otra máquina que resuelve el mismo problema en tiempo c\cdot f(n).

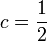
Esbozo de prueba para c=\frac{1}{2}

Suponga que la máquina de Turing M resuelve el problema en f(n) pasos y que tiene k símbolos de cinta y s estados internos. Construya una nueva máquina M' con k3 símbolos de cinta donde cada símbolo representa un grupo de 3 símbolos adyacentes en la máquina M.

La cinta de la máquina M' es una representación comprimida de la cinta de la máquina M, donde la célula i en la máquina M' representa la secuencia de células 2i − 1, 2i y 2i + 1 de la máquina M (note que estos grupos coinciden parcialmente).

En un paso computacional, M' simula la computación de M hasta que la cabeza de M' salga del grupo de células a la izquierda o la derecha (esta simulación se puede hacer en un solo paso porque M no puede estar en más de sk3 estados sin que salga del cacho o repita un estado). Durante esta simulación puede que M acepte, en cual caso M' también acepta, o puede que M rodee, en cual caso M' no hace nada (y así también rodee).

Una sutileza final es que porque los cachos se solapan, cada transición entre cachos en M debe ser transformado en k transiciones entre células en M' para tomar en cuenta la k símbolos diferentes que se podría haber escrito en la célula que pertenece a los dos cachos. La construcción requiere que cada paso computacional en M' corresponde a por lo menos 2 pasos en M. Entonces M' toma no más de 1 / 2f(n) pasos. Por añadir pasos que demoran en M', podemos asegurar que tome exactamente 1 / 2f(n) pasos.

Debe ser fácil ver como generalizar la prueba a todos los valores de c, y también que la prueba aplica tanto al espacio como al tiempo.

El teorema del aumento de velocidad linear es la razón que la teoría de complejidad hace caso omiso de factores lineares y representa la complejidad de algoritmos con la cota superior asintótica

Obtenido de "Teorema del aumento de velocidad lineal"

Wikimedia foundation. 2010.

Игры ⚽ Поможем сделать НИР

Mira otros diccionarios:

  • Teorema del aumento de velocidad — En la teoría de la complejidad computacional, un teorema del aumento de velocidad es un teorema que considera un algoritmo que resuelva un problema y demuestra que existe otro algoritmo más rápido que resuelve el mismo problema (o, más… …   Wikipedia Español

  • Teorema del incremento lineal de velocidad — El teorema del incremento lineal de velocidad de las máquinas de Turing es un teorema de teoría de la complejidad computacional, que se puede enunciar: Dado c > 0 y cualquier máquina de Turing que resuelve un problema en tiempo , hay otra… …   Wikipedia Español

  • Teorema de Bell — El teorema de Bell o desigualdades de Bell se aplica en mecánica cuántica para cuantificar matemáticamente las implicaciones planteadas teóricamente en la paradoja de Einstein Podolsky Rosen y permitir así su demostración experimental. Debe su… …   Wikipedia Español

  • Historia del electromagnetismo — La Historia del electromagnetismo, que es el conocimiento y el uso registrado de las fuerzas electromagnéticas, data de hace más de dos mil años. En la antigüedad ya estaban familiarizados con los efectos de la electricidad atmosférica, en… …   Wikipedia Español

  • Filosofía del espacio y el tiempo — Saltar a navegación, búsqueda La filosofía del espacio y el tiempo es la rama de la filosofía que trata de los aspectos referidos a la ontología, la epistemología y la naturaleza del espacio y el tiempo, lo que se conoce también como cosmología.… …   Wikipedia Español

  • Flujo sanguíneo — Saltar a navegación, búsqueda Contenido 1 Definición. 2 Introducción 2.1 Valores normales en el humano 2.2 Índice c …   Wikipedia Español

  • Sobredotación intelectual — Saltar a navegación, búsqueda La sobredotación intelectual es el termino con el que en países de habla hispana se ha identificado a las personas con una capacidad intelectual por encima de la media. Asimismo, superdotado es el término usado para… …   Wikipedia Español

  • Efectos de las armas nucleares — Saltar a navegación, búsqueda Contenido 1 Explosiones nucleares hasta la fecha 2 Efectos inmediatos 3 La Zona Cero …   Wikipedia Español

  • IK Pegasi — Localización de IK Pegasi. Datos de observación (Época …   Wikipedia Español

  • Ciencia — La ciencia (del latín scientia conocimiento ) es el conjunto de conocimientos sistemáticamente estructurados, y susceptibles de ser articulados unos con otros. El árbol de la ciencia. Interpretación bíblica Contenido …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”