Teorema del cateto

Teorema del cateto
Figura 1 - Los segmentos m y n son las respectivas proyecciones de los lados b y a sobre la hipotenusa c, siendo h la altura correspondiente a la hipotenusa.

El teorema del cateto establece lo siguiente:

Teorema del cateto

En todo triángulo rectángulo el cuadrado de un cateto es igual al producto de la hipotenusa por la proyección de dicho cateto sobre la misma.

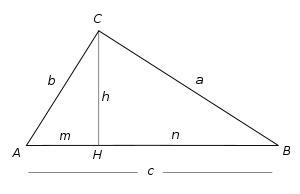
Este teorema (véase Figura 1) puede expresarse matemáticamente —para cada uno de sus dos catetos— como:

b^2 \ =\ c\; m

a^2 \ =\ c\; n

Donde m y n son, respectivamente, las proyecciones de los catetos b y a sobre la hipotenusa c.

Demostración

Sea el triángulo ΔABC rectángulo en C, dispuesto de modo que su base es la hipotenusa c. La altura h determina los segmentos m y n, que son, respectivamente, las proyecciones de los catetos b y a sobre la hipotenusa.

Los triángulos rectángulos ΔABC, ΔACH y ΔBCH tienen iguales sus ángulos, y por lo tanto son semejantes:

  1. Todos tienen un ángulo recto.
  2. Los ángulos B y ACH son iguales por ser agudos, por abarcar un mismo arco, y tener sus lados perpendiculares.
  3. Igualmente sucede con los ángulos A y BCH.
Figura 1 - Los segmentos m y n son las respectivas proyecciones de los lados b y a sobre la hipotenusa c, siendo h la altura correspondiente a la hipotenusa.

Puesto que en las figuras semejantes los lados homólogos son proporcionales, tendremos que:


  • Por la semejanza entre los triángulos ΔACH y ΔABC
\frac {b}{m}=\frac {c}{b}


de dónde,


b^2 \ =\ cm


  • Por la semejanza entre los triángulos ΔBCH y ΔABC


\frac {a}{n}=\frac {c}{a}


a^2 \ =\ cn


y el teorema queda demostrado.

== Corolario ==

(Corolario 1) “En todo triángulo rectángulo la longitud de la proyección ortogonal de cualquier cateto sobre la hipotenusa es igual al cuadrado de la longitud de ese mismo cateto dividido por la longitud de la hipotenusa.”

Basados en las dos ecuaciones del teorema anterior, para deducir el «corolario 1» basta con despejar en cada una de ellas, la respectiva variable de su proyección ortogonal, siendo éstas m y n:

b^2 \ =\ c\; m \;\;\;\; ; \;\;\;\; a^2 \ =\ c\; n

en las que al despejar respectivamente m y n producen las ecuaciones del «corolario 1»:

m=\frac{b^2}{c} \;\;\;\; ; \;\;\;\; n=\frac{a^2}{c}

donde m es la proyección ortogonal del cateto b sobre la hipotenusa c (véase figura 1) y n es la proyección ortogonal del cateto a también sobre la hipotenusa c.

Véase también


Wikimedia foundation. 2010.

Игры ⚽ Поможем решить контрольную работу

Mira otros diccionarios:

  • Teorema de la altura — En matemáticas, el teorema de la altura de un triángulo rectángulo establece que: Teorema de la altura (forma 1) En cualquier triángulo rectángulo la altura relativa a la hipotenusa es la media proporcional entre las proyecciones ortogonales de… …   Wikipedia Español

  • Teorema de Pitágoras — El Teorema de Pitágoras establece que en un triángulo rectángulo, el área del cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de las áreas del cuadrado de los catetos (los dos lados menores del… …   Wikipedia Español

  • Cateto — Saltar a navegación, búsqueda Un cateto, en geometría, es cualquiera de los dos lados menores de un triángulo rectángulo –los que conforman el ángulo recto. El lado mayor se denomina hipotenusa –el que es opuesto al ángulo recto. En los… …   Wikipedia Español

  • cateto — {{＃}}{{LM C07651}}{{〓}} {{SynC07826}} {{［}}cateto{{］}}, {{［}}cateta{{］}} ‹ca·te·to, ta› {{《}}▍ s.{{》}} {{＜}}1{{＞}} {{※}}desp.{{¤}} Persona rústica y sin refinamiento. {{《}}▍ s.m.{{》}} {{＜}}2{{＞}} {{♂}}En un triángulo rectángulo,{{♀}} cada uno de… …   Diccionario de uso del español actual con sinónimos y antónimos

  • Triángulo — Para otros usos de este término, véase Triángulo (desambiguación). El triángulo es un polígono de tres lados. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran… …   Wikipedia Español

  • Identidades trigonométricas — Este artículo o sección sobre matemáticas necesita ser wikificado con un formato acorde a las convenciones de estilo. Por favor, edítalo para que las cumpla. Mientras tanto, no elimines este aviso puesto el 9 de abril de 2011. También puedes… …   Wikipedia Español

  • Triángulo sagrado egipcio — o Triángulo egipcio,[1] es el nombre moderno dado a un triángulo rectángulo cuyo lados tienen las longitudes 3, 4 y 5, o sus medidas guardan estas proporciones. Es el triángulo rectángulo más fácil de construir y, posiblemente, se utilizó para… …   Wikipedia Español

  • Función trigonométrica — En matemáticas, Las funciones trigonométricas son las funciones que se definen a fin de extender la definición de las razones trigonométricas a todos los números reales. Las funciones trigonométricas son de gran importancia en física, astronomía …   Wikipedia Español

  • Triángulo de Kepler — fig. tk1: El triángulo de Kepler es un triángulo rectángulo formado por tres cuadrados con áreas en progresión geométrica de acuerdo al número áureo. El triángulo de Kepler es un triángulo rectángulo con lados en progresión geométrica. La… …   Wikipedia Español

  • Filosofía de la matemática — Saltar a navegación, búsqueda La filosofía de las matemáticas es una rama de la filosofía. Según Michael Dummett puede considerarse que hay cuatro preguntas fundamentales sobre el contenido de la filosofía de las matemáticas: ¿Cómo sabemos que… …   Wikipedia Español

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”