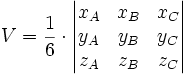- Tetraedro (general)
-
Tetraedro (general)
Un tetraedro es un poliedro de cuatro caras. Con este número de caras ha de ser forzosamente un poliedro convexo, y sus caras triangulares, encontrándose tres de ellas en cada vértice. Si las cuatro caras del tetraedro son triángulos equiláteros, forzosamente iguales entre sí, el tetraedro se denomina regular.
Propiedades geométricas
En todo tetraedro, sea o no regular, se verifica que: DAEC _ HAR
- Los segmentos que unen los puntos medios de los tres pares de aristas opuestas son concurrentes en un punto, que los divide por su mitad.
- Los segmentos que unen cada vértice con los puntos de intersección de las medianas de su cara opuesta son también concurrentes en un punto, que los divide separando tres cuartas partes del lado del vértice respectivo (Teorema de Commandinho).
- Los seis planos perpendiculares a las aristas por sus puntos medios pasan por un mismo punto, centro de la esfera circunscrita al tetraedro.
- Las rectas perpendiculares a las caras por su circuncentro son concurrentes en un punto, centro de la esfera circunscrita al tetraedro.
- Los planos bisectores de los diedros interiores de un tetraedro concurren en un punto equidistante de las cuatro caras, centro de la esfera inscrita al tetraedro.
- Las alturas de un tetraedro sólo son concurrentes si las aristas opuestas son perpendiculares.
Volumen
Existe una fórmula general para el cálculo del volumen de un tetraedro, sea o no regular, en función de las coordenadas cartesianas (x, y, z) de tres de sus vértices A, B y C (supuesto el origen de coordenadas en el cuarto):
Otra fórmula, que puede obtenerse de la anterior, permite calcular el volumen de un tetraedro, regular o irregular, conociendo la longitud de dos aristas opuestas,
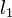 y
y 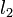 y la distancia entre ambas
y la distancia entre ambas 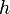 , y es :
, y es :
Esta fórmula es aplicable para calcular, de forma aproximada, el volumen de un terraplén, de una carretera o una presa de materiales sueltos, por ejemplo, a partir de la longitud de su coronación
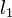 , la longitud en la base
, la longitud en la base 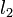 , y su altura
, y su altura 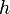 .Categorías: Wikipedia:Fusionar | Poliedros
.Categorías: Wikipedia:Fusionar | Poliedros
Wikimedia foundation. 2010.