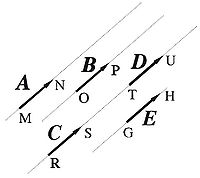
Vector equipolente

Condiciones de equipolencia.

Decimos que dos o más vectores son equipolentes cuando las magnitudes físicas que representan tienen el mismo valor y producen los mismos efectos.

Clasificacion de las magnitudes vectoriales

En general, para que dos o más vectores sean iguales (equipolentes) no basta que tengan el mismo módulo, la misma dirección y el mismo sentido.

Las condiciones de equipolencia, más o menos restrictivas, permiten clasificar las magnitudes vectoriales en tres clases o categorías.

Vectores libres. Las condiciones de equipolencia consideran que dos direcciones son equivalentes con tal de que sean paralelas. Por consiguiente, diremos que dos vectores libres son iguales si tienen el mismo módulo, la misma dirección y el mismo sentido, aunque sus rectas de acción (directrices) sean diferentes. De este modo, en la Figura son equipolentes los vectores

Ejemplos: la velocidad y la aceleración de una partícula, , el momento de un par,...

Vectores deslizantes. Las condiciones de equipolencia imponen que los vectores tengan el mismo módulo y que actúen en un mismo sentido sobre una misma recta de acción (recta directriz), siendo indiferente el punto de la recta en que estén aplicados. Reciben esta denominación porque los vectores pueden deslizar a lo largo de su recta de acción sin cambiar los efectos asociados a la magnitud física que representan. Así, en la Figura 1.1, tan sólo es

Ejemplos: las fuerzas que actúan sobre un sólido rígido, la velocidad angular del sólido rígido,...

Vectores ligados. Las condiciones de equipolencia son aún más restrictivas ya que imponen que los vectores tengan el mismo módulo, que actúen en un mismo sentido sobre una misma recta de acción (recta directriz) y estén aplicados en un mismo punto. Obviamente, los vectores no pueden desplazarse paralelamente ni deslizar, por lo que está ligados a un punto. En la figura, cada uno de los vectores tan sólo es equipolente consigo mismo.

Ejemplos: intensidad del campo gravitatorio (), intensidad del campo eléctrico ()

Referencias

Véase también

Bibliografía

• Ortega, Manuel R. (1989-2006) (en español). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. 
• Resnick,Robert & Krane, Kenneth S. (2001) (en inglés). Physics. New York: John Wiley & Sons. ISBN 0-471-32057-9. 

Enlaces externos

• Buscon.Rae.es (Diccionario de la lengua española, de la Real Academia Española).