Vector multidimensional

En programación, un vector multidimensional es un vector que se indexa mediante una lista ordenada de enteros. El número de enteros que se utiliza en esta lista para indexar el vector multidimensional es siempre el mismo y se conoce como la dimensionalidad del vector. Por otra parte, los límites de cada uno de los enteros que forman parte del indice, determinan la dimensión del vector. A un vector con dimensionalidad k se le suele llamar k-dimensional. Los vectores 1-dimensional se corresponden con los vectores ordinarios en los que los elementos están dispuestos en una única fila (o columna); los vectores 2-dimensional son otra forma de llamar a las clásicas matrices en las que sus elementos están dispuestos en varias filas y columnas (dos dimensiones). En la práctica, la dimensionalidad de un vector raras veces excede de tres.

Representación en memoria

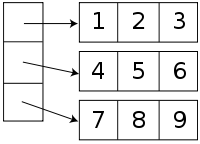
La forma de disponer los elementos de un vector 1-dimensional en la memoria de un ordenador es trivial, ya que ésta, en sí misma, tiene la forma de un vector 1-dimensional (muy grande). Cuando se quiere almacenar vectores n-dimensionales, sin embargo, el problema ya no es evidente. Supongamos que queremos representar esta simple matriz de dos dimensiones:

La forma más común de indexar esta matriz (o vector 2-dimensional) es utilizando la convención RC (del inglés Row-Column, fila-columna), en la que los elementos se referencian indicando primero la fila y luego la columna (ejemplo, ), de esta forma se tiene que:

La indexación de vectores multidimensionales se puede hacer de alguna de estas maneras:

• Orden fila-principal: Los elementos de cada fila son almacenados en orden, primero una fila, luego otra, y así sucesivamente. Este método se utiliza sobre todo en los arrays estáticos declarados en C.

• Orden columna-principal: Análogo al anterior pero esta vez almacenando los elementos por columnas en vez de por filas:

Vector 2-dimensional almacenado en un vector 1-dimensional de vectores 1-dimensionales.

• Vector de vectores (o array de arrays): Típicamente, los vectores multidimensionales se representan utilizando un vector 1-dimensional que contiene referencias (o punteros) a otros vectores 1-dimensionales. Estos subvectores pueden ser, indistintamente, las filas o las columnas de la matriz, todo depende del criterio o la interpretación que se quiera tomar.

Las dos primeras formas son más compactas y tienen potencialmente mejor localización de referencia, pero también son más limitadas; los vectores deben ser rectangulares, en el sentido de que ninguna fila puede contener más elementos otra. Los vectores de vectores, por otro lado, permiten la creación de vectores desiguales, también llamados vectores dentados, en la que el rango válido de un índice depende del valor de otro, o dicho con otras palabras, que las diferentes filas (o columnas) pueden ser de diferentes tamaños. Los vectores de vectores también son de utilidad en los lenguajes de programación que sólo permiten vectores 1-dimensionales como primitivas.

En muchas aplicaciones, como aplicaciones numéricas que trabajan con matrices, hay que iterar sobre vectores rectangulares 2-dimensionales de forma predecible. Por ejemplo, calcular un elemento de la matriz producto A x B implica iterar sobre una fila de A y una columna de B simultáneamente. Al indexar los elementos de la matriz según se encuentre esta almacenada en memoria, se deben optimizar las operaciones de localización de cada elemento tanto como se pueda. A veces, un compilador puede determinar automáticamente el diseño de la serie secuencial de elementos de un vector para que se almacenen también secuencialmente en memoria, en nuestro ejemplo, podría elegir el orden de fila-principal para A, y el orden columna-principal para B. Existen más formas de almacenar los elementos de una matriz en memoria, que serán más eficientes para otro tipo de problemas, por ejemplo si se quiere iterar sobre la diagonal principal de una matriz.

Véase también

• Vector (programación)
• Vector (física)
• Álgebra lineal
• Estructura de datos
• Base de datos multidimensional
• Gráfico vectorial
• Cubo OLAP