Álgebra lineal

Álgebra lineal: El álgebra lineal es la rama de las matemáticas que estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y en un enfoque más formal, espacios vectoriales, y sus transformaciones lineales.

Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.

La historia del álgebra lineal moderna se remonta a los años de 1843 cuando William Rowan Hamilton (de quien proviene el uso del término vector) creó los cuaterniones; y de 1844 cuando Hermann Grassmann publicó su libro Die lineare Ausdehnungslehre (La teoría lineal de extensión).

Contenido

1 Conceptos básicos

2 Contexto general

3 Espacios vectoriales de uso común

3.1 Vectores en Rⁿ

3.2 Matrices

3.3 Espacio vectorial de polinomios en una misma variable

4 Generalización y temas relacionados

5 Véase también

6 Enlaces externos

Conceptos básicos

Representación gráfica de la suma de dos vectores en $\mathbb{R}^2$ .

Para ilustrar los conceptos básicos estudiados en el álgebra lineal suele tomarse como ejemplo el espacio vectorial $\mathbb{R}^{n}$ (conocido también como espacio vectorial real de dimensión n, es decir, un espacio formado por vectores de n componentes) por ser el más simple y a la vez el más usado en aplicaciones de uso.

Los objetos básicos de estudio son las n-tuplas ordenadas de números reales $(x_1, x_2,\ldots, x_n)$ que se denominan vectores y el conjunto de todos los vectores con n elementos forma un espacio vectorial $\mathbb{R}^{n}$ .

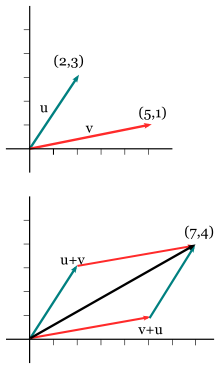
Así, por ejemplo, el vector (4.5, 7/11, -8) es un vector del espacio $\mathbb{R}^3$ y (6, -1, 0, 2, 4) es un elemento de $\mathbb{R}^5$ . En particular, $\mathbb{R}^2$ corresponde a un plano cartesiano XY y $\mathbb{R}^3$ es el espacio euclidiano provisto de un sistema de coordenadas XYZ.

Las operaciones básicas entre los vectores (en lo que concierne al álgebra lineal) son dos: la suma de vectores y el producto por escalar.

El producto por un escalar en $\mathbb{R}^{n}$ sigue la regla:

$r \cdot (x_1, x_2,\ldots, x_n)=(rx_1, rx_2,\ldots, rx_n).$

La interpretación gráfica del producto por escalar es una contracción o dilatación del vector (dependiendo de la magnitud del escalar, es decir, si $\ r$ es mayor o menor de 1), junto con una posible inversión de su sentido (si el signo es negativo, es decir, si $\ r$ es mayor o menor de 0).

Las funciones $\ T$ de interés para el álgebra lineal, entre los espacios vectoriales descritos, son aquellas que satisfacen las dos condiciones siguientes con la operaciones básicas para todo par de vectores $\mathbf{u,v}$ y todo escalar $\ r$ :

$T(\mathbf{u+v})=T(\mathbf{u}) + T(\mathbf{v}),\qquad T(r\cdot \mathbf{u})=r\cdot T(\mathbf{u}).$

Las funciones que cumplen las condiciones anteriores se denominan transformaciones lineales y en el ejemplo que estamos usando corresponden a vectores de números reales, pero puede extenderse a matrices del espacio $\mathbb{R}^{n}\times\mathbb{R}^{m}$ que son las matrices de números reales de tamaño $n\times m$ .

El álgebra lineal estudia entonces las distintas propiedades que poseen estos conceptos y las relaciones entre los mismos. Por ejemplo, estudia cuándo una "ecuación" de la forma Au=v (donde u,v son vectores y A es una matriz) tiene solución, problema que es equivalente a determinar si un sistema de ecuaciones lineales tiene solución o no.

Contexto general

De manera más formal, el álgebra lineal estudia conjuntos denominados espacios vectoriales, los cuales constan de un conjunto de vectores y un conjunto de escalares (que tiene estructura de campo, con una operación de suma de vectores y otra de producto entre escalares y vectores que satisfacen ciertas propiedades (por ejemplo, que la suma es conmutativa).

Estudia también transformaciones lineales, que son funciones entre espacios vectoriales que satisfacen las condiciones de linealidad:

$T(u+v)=T(u) + T(v),\qquad T(r\cdot u)=r\cdot T(u).$

A diferencia del ejemplo desarrollado en la sección anterior, los vectores no necesariamente son n-adas de escalares, sino que pueden ser elementos de un conjunto cualquiera (de hecho, a partir de todo conjunto puede construirse un espacio vectorial sobre un campo fijo).

Finalmente, el álgebra lineal estudia también las propiedades que aparecen cuando se impone estructura adicional sobre los espacios vectoriales, siendo una de las más frecuentes la existencia de un producto interno (una especie de producto entre dos vectores) que permite introducir nociones como longitud de vectores y ángulo entre un par de los mismos...

Espacios vectoriales de uso común

Dentro de los espacios vectoriales de dimensión finita, son de amplio uso los tres tipos siguientes de espacios vectoriales:

Vectores en Rⁿ

Este espacio vectorial está formado por el conjunto de vectores de n dimensión (es decir con n número de componentes). Podemos encontrar un ejemplo de ellos en los vectores R² , que son famosos por representar las coordenadas cartesianas: (2,3), (3,4),...

Matrices $m \times n$

Artículo principal: Matriz (matemática)

Es un arreglo rectangular de números, símbolos o expresiones, cuyas dimensiones son descritas en las cantidades de filas (usualmente m) por las de columnas (n) que poseen. Los arreglos matriciales son particularmente estudiados por el álgebra lineal y son bastantes usados en las ciencias e ingeniería.

Espacio vectorial de polinomios en una misma variable

Un ejemplo espacio vectorial está dado por todos los polinomios cuyo grado es menor o igual a 2 con coeficientes reales sobre una variable x.

Ejemplos de tales polinomios son:

$4x^2-5x+1,\quad \frac{2x^2}{7}-3,\quad 8x+4,\quad 5$

La suma de dos polinomios cuyo grado no excede a 2 es otro polinomio cuyo grado no excede a 2:

$(3 x 2 - 5 x + 1) + (4 x - 8) = 3 x 2 - x - 7$

El campo de escalares es naturalmente el de los números reales, y es posible multiplicar un número por un polinomio:

$5\cdot(2x + 3) = 10x + 15$

donde el resultado nuevamente es un polinomio (es decir, un vector).

Un ejemplo de transformación lineal es el operador derivada D, que asigna a cada polinomio el resultado de derivarlo:

$D (3 x 2 - 5 x + 7) = 6 x - 5.$

El operador derivada satisface las condiciones de linealidad, y aunque es posible demostrarlo con rigor, simplemente lo ilustramos con un ejemplo la primera condición de linealidad:

$D ((4 x 2 + 5 x - 3) + (x 2 - x - 1)) = D (5 x 2 + 4 x - 4) = 10 x + 4$

y por otro lado:

$D (4 x 2 + 5 x - 3) + D (x 2 - x - 1) = (8 x + 5) + (2 x - 1) = 10 x + 4.$

Cualquier espacio vectorial tiene una representación en coordenadas similar a $\mathbb{R}^n$ , lo cual se obtiene mediante la elección de una base (álgebra) (es decir, un conjunto especial de vectores), y uno de los temas recurrentes en el álgebra lineal es la elección de bases apropiadas para que los vectores de coordenadas y las matrices que representan las transformaciones lineales tengan formas sencillas o propiedades específicas.

Generalización y temas relacionados

Puesto que el álgebra lineal es una teoría exitosa, sus métodos se han desarrollado por otras áreas de la matemática: en la teoría de módulos, que remplaza al cuerpo en los escalares por un anillo; en el álgebra multilineal, uno lidia con 'múltiples variables' en un problema de mapeo lineal, en el que cada número de las diferentes variables se dirige al concepto de tensor; en la teoría del espectro de los operadores de control de matrices de dimensión infinita, aplicando el análisis matemático en una teoría que no es puramente algebraica. En todos estos casos las dificultades técnicas son mucho más grandes.

Véase también

Portal:Matemática. Contenido relacionado con Matemática.

Enlaces externos

Wikimedia Commons alberga contenido multimedia sobre Álgebra lineal. Commons

Álgebra lineal por Elmer G. Wiens (en inglés)

Álgebra Lineal: Conceptos Básicos

Introducción al Álgebra Lineal en Contexto por José Arturo Barreto

Categoría:
Álgebra lineal

Игры ⚽ Нужен реферат?

Mira otros diccionarios:

Álgebra lineal — El Álgebra Lineal es la rama de las matemáticas que concierne al estudio de vectores, espacios vectoriales, transformaciones lineales, y sistemas de ecuaciones lineales. Los espacios vectoriales son un tema central en las matemáticas modernas;… … Enciclopedia Universal
Álgebra lineal numérica — El Álgebra lineal numérica es el estudio de algoritmos para realizar cálculos de álgebra lineal, en particular las operaciones con matrices, en las computadoras. A menudo es una parte fundamental de la ingeniería y los problemas de ciencias de la … Wikipedia Español
Invariante algebraico (álgebra lineal) — Un invariante algebraico es una función polinómica de las componentes de la matriz de una aplicación lineal, no depende de la base vectorial escogida para representar la aplicación lineal en forma de matriz. En otras palabras, un invariante… … Wikipedia Español
Lineal — Para otros usos de este término, véase Lineal (distribución comercial). La palabra lineal viene de la palabra latín linearis, que significa creado por líneas . Contenido 1 Matemáticas (función lineal) 1.1 Propiedades 1.2 … Wikipedia Español
Álgebra multilineal — En la matemática, el álgebra multilineal es una área de estudio que generaliza los métodos del álgebra lineal. Los objetos de estudio son los productos tensoriales de espacios vectoriales y las transformaciones multi lineales entre los espacios.… … Wikipedia Español
lineal — ► adjetivo 1 De la línea: ■ los trazos lineales representan las calles; tiene una asignatura de dibujo lineal. 2 BOTÁNICA, ZOOLOGÍA Que tiene forma larga y estrecha: ■ los pinos tienen hojas lineales. 3 Que es proporcional: ■ se ha producido un… … Enciclopedia Universal
Álgebra — (Del lat. vulgar algebra < ár. al yebr, reducción, álgebra matemática.) ► sustantivo femenino 1 MATEMÁTICAS Parte de las matemáticas que estudia las estructuras que generalizan la solución de problemas aparentemente inconexos. 2 MATEMÁTICAS… … Enciclopedia Universal
Álgebra de Clifford — Las álgebras de Clifford son álgebras asociativas de importancia en matemáticas, en particular en teoría de la forma cuadrática y del grupo ortogonal y en la física. Se nombran así por William Kingdon Clifford. Definición formal Sea V un espacio… … Wikipedia Español
Álgebra sobre un cuerpo — En matemáticas, un álgebra sobre un cuerpo K, o una K álgebra, es un espacio vectorial A sobre K equipado con una noción compatible de multiplicación de elementos de A. Una generalización directa admite que K sea cualquier anillo conmutativo.… … Wikipedia Español
Álgebra de Virasoro — El álgebra de Virasoro es una forma de álgebra de Lie compleja, dada como extensión central del campo vectorial de los polinomios complejos sobre la circunferencia unitaria; esta álgebra toma su nombre del físico argentino Miguel Ángel Virasoro.… … Wikipedia Español

Marcar y compartir
Buscar en todos diccionarios
Traducir
Buscar en la internet

Compartir el artículo y extractos