Vector

Vector
Para otros usos de este término, véase Vector (desambiguación).
Este artículo trata sobre el concepto físico de vector. Para el tratamiento matemático formal, véase Espacio Vectorial.
Un vector desde A hasta B.

En física, matemáticas e ingeniería, un vector (también llamado vector euclidiano o vector geométrico) es una herramienta geométrica utilizada para representar una magnitud física definida por un módulo (o longitud) y una dirección (u orientación).[1] [2] [3] [4]

Los vectores se pueden representar geométricamente como segmentos de recta dirigidos o flechas en el plano \R^2 o en el espacio \R^3.

Ejemplos:

  • La velocidad con que se desplaza un móvil es una magnitud vectorial, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección hacia la que se dirige.
  • La fuerza que actúa sobre un objeto es una magnitud vectorial, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que opera.

Contenido

Conceptos fundamentales

Esta sección explica los aspectos básicos, la necesidad de los vectores para representar ciertas magnitudes físicas, los componentes de un vector, la notación de los mismos, etc.

Definición

Se llama vector de dimensión n \, a una tupla de n \, números reales (que se llaman componentes del vector). El conjunto de todos los vectores de dimensión n \, se representa como \mathbb{R}^n (formado mediante el producto cartesiano).

Así, un vector v \, perteneciente a un espacio \mathbb{R}^n se representa como: v \in \mathbb{R}^n, donde v = (a_1, a_2, a_3, \dots, a_n).

Un vector también se puede ver desde el punto de vista de la geometría como vector geométrico (usando frecuentemente el espacio tridimensional \mathbb{R}^3 ó bidimensional \mathbb{R}^2).

Un vector fijo del plano es un segmento orientado, en el que hay que distinguir dos características:[1] [2] [3]

  • dirección: la orientación de la recta
  • módulo: la longitud del segmento

Los vectores fijos del plano se denotan con dos letras mayúsculas, por ejemplo AB, que indican su origen y extremo respectivamente.

\overrightarrow{AB} = (x_B - x_A, y_B - y_A) \,

Magnitudes escalares y vectoriales

Representación gráfica de una magnitud vectorial, con indicación de su punto de aplicación y de los versores cartesianos.
Representación de los vectores.

Frente a aquellas magnitudes físicas, tales como la masa, la presión, el volumen, la energía, la temperatura, etc; que quedan completamente definidas por un número y las unidades utilizadas en su medida, aparecen otras, tales como el desplazamiento, la velocidad, la aceleración, la fuerza, el campo eléctrico, etc., que no quedan completamente definidas dando un dato numérico, sino que llevan asociadas una dirección. Estas últimas magnitudes son llamadas vectoriales en contraposición a las primeras llamadas escalares.

Las magnitudes escalares quedan representadas por el ente matemático más simple; por un número. Las magnitudes vectoriales quedan representadas por un ente matemático que recibe el nombre de vector. En un espacio euclidiano, de no más de tres dimensiones, un vector se representa por un segmento orientado. Así, un vector queda caracterizado por los siguientes elementos: su longitud o módulo, siempre positivo por definición, y su dirección, la cual puede ser representada mediante la suma de sus componentes vectoriales ortogonales, paralelas a los ejes de coordenadas; o mediante coordenadas polares, que determinan el ángulo que forma el vector con los ejes positivos de coordenadas.[5] [6]

Se representa como un segmento orientado, con una dirección, dibujado de forma similar a una "flecha". Su longitud representa el módulo del vector y la "punta de flecha" indica su dirección.[1] [2] [3]

Notación

Commons-emblem-question book orange.svg
 Este artículo o sección necesita referencias que aparezcan en una publicación acreditada, como revistas especializadas, monografías, prensa diaria o páginas de Internet fidedignas.
Puedes añadirlas así o avisar al autor principal del artículo en su página de discusión pegando: {{subst:Aviso referencias|Vector}} ~~~~

Las magnitudes vectoriales se representan en los textos impresos por letras en negrita, para diferenciarlas de las magnitudes escalares que se representan en cursiva. En los textos manuscritos, las magnitudes vectoriales se representan colocando una flecha sobre la letra que designa su módulo (el cual es un escalar). Ejemplos:

  • \mathbf A, \ \mathbf a,\ \boldsymbol{\omega}, ... representan, respectivamente, las magnitudes vectoriales de módulos A, a, ω, ... El módulo de una magnitud vectorial también se representa encerrando entre barras la notación correspondiente al vector: |\mathbf A|, \ |\mathbf a\,\ |\boldsymbol{\omega}|, ...
  • En los textos manuscritos se escribe: \vec A, \ \vec a,\ \vec{\omega},... para los vectores y |\vec A|, \ |\vec a|,\ |\vec {\omega}|,... o A, \ a,\ {\omega},... para los módulos.

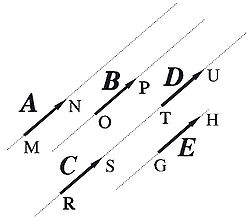
Cuando convenga, se representan la magnitud vectorial haciendo referencia al origen y al extremo del segmento orientado que la representa geométricamente; así, se designan los vectores representados en la Figura 2 en la forma \mathbf A = \overrightarrow{MN}, \mathbf B = \overrightarrow{OP} \,, ... resultando muy útil esta notación para los vectores que representan el desplazamiento.

Además de estas convenciones los vectores unitarios o versores, cuyo módulo es la unidad, se representan frecuentemente con un circunflejo encima, por ejemplo \mathbf{\hat{u}}, \mathbf{\hat{v}}.

Clasificación de vectores

Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse distintos tipos de los mismos:

  • Vectores libres: no están aplicados en ningún punto en particular.
  • Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
  • Vectores fijos o ligados: están aplicados en un punto en particular.

Podemos referirnos también a:

  • Vectores unitarios: vectores de módulo unidad.
  • Vectores concurrentes: sus rectas de acción concurren en un punto propio o impropio (paralelos).
  • Vectores opuestos: vectores de igual magnitud, pero dirección contraria.
  • Vectores colineales: los vectores que comparten una misma recta de acción.
  • Vectores coplanarios: los vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).

Componentes de un vector

Componentes del vector.

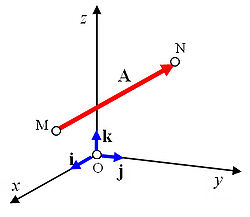
Un vector en el espacio se puede expresar como una combinación lineal de tres vectores unitarios o versores perpendiculares entre sí que constituyen una base vectorial.

En coordenadas cartesianas, los vectores unitarios se representan por \mathbf{i} \,, \mathbf{j} , \mathbf{k} , paralelos a los ejes de coordenadas x, y, z positivos. Las componentes del vector en una base vectorial predeterminada pueden escribirse entre paréntesis y separadas con comas:

\mathbf{a} = (a_x,a_y,a_z)

o expresarse como una combinación de los vectores unitarios definidos en la base vectorial. Así, en un sistema de coordenadas cartesiano, será

\mathbf{a} = a_x \, \mathbf{i}+ a_y \, \mathbf{j} + a_z \, \mathbf{k}

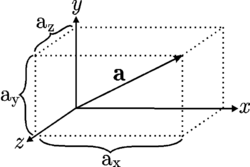
Estas representaciones son equivalentes entre sí, y los valores ax, ay, az, son las componentes de un vector que, salvo que se indique lo contrario, son números reales.

Una representación conveniente de las magnitudes vectoriales es mediante un vector columna o un vector fila, particularmente cuando están implicadas operaciones matrices (tales como el cambio de base), del modo siguiente:

\mathbf{a} = \begin{bmatrix} a_x\\ a_y\\ a_z\\ \end{bmatrix} \qquad \mathbf{a} = [ a_x\ a_y\ a_z ]

Con esta notación, los vectores cartesianos quedan expresados en la forma:

{\mathbf i} = [1\ 0\ 0],\ {\mathbf j} = [0\ 1\ 0],\ {\mathbf k} = [0\ 0\ 1]

Representación gráfica de vectores

Aunque hay quien no recomienda el uso de gráficos para evitar la confusión de conceptos y la inducción al error, sin investigación que lo corrobore, también es cierto que la memoria se estimula con mejores resultados. Para ello veamos las notas:

  • Llamaremos vector a la representación visual con el símbolo de flecha( un segmento y un triángulo en un extremos).
  • La rectitud visual de una flecha o curvatura de la misma, no la hace diferente en símbolo si los dos extremos permanecen en el mismo lugar y orden.
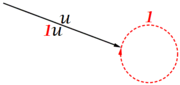
  • El que una flecha cierre en sí misma, indica la ausencia de efectos algebraicos.
  • Para visualizar la suma de vectores se hará encadenándolos, es decir, uniendo el extremo que tiene un triángulo(final) del primer vector con el extremo que no lo tiene(origen) del segundo vector manteniendo la dirección y distancia, propias al espacio, de sus dos extremos, ya que estas dos cualidades los distingue visualmente de otros vectores.

Examinemos cada uno de los casos que aparecen en la definición:

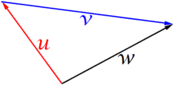
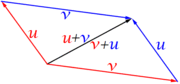
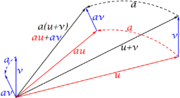
La definición suma de vectores en el orden u+v produce otro vector, es como encadenar, siempre visualmente, un vector u y luego uno v. Diremos que u+v se simplifica como un vector w o que w descompone como suma de vectores u y v.
Vetorial space P.GIF
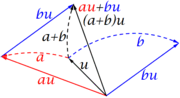
1) Decir que u+v=v+u, es exigir que las dos sumas simplifiquen en el mismo vector, en negro. Véase que en física los vectores en rojo simulan la descomposición de fuerzas ejercidas por el vector negro en su origen, y se representa con un paralelogramo.
Vectorial space P 1.GIF
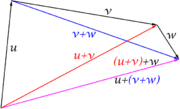
2) Decir que u+(v+w)=(u+v)+w, es exigir que las simplificaciones de sumas de vectores puedan ser optativas en cualquier cadena de sumas.
Vectorial space P 2.GIF
3) Decir que existe un vector 0 tal que u+0=u, equivale a exigir que exista un vector incapaz de efectuar, mediante la suma, modificación alguna a todos los vectores.
Vectorial space P 3.GIF
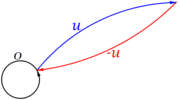
4) Decir que u+(-u)=0, es exigir la existencia de un elemento, -u, que sumado a u simplifique en un vector cero.
Vectorial space P 4.GIF
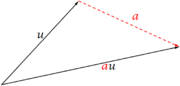
La definición producto por escalar a \cdot u produce otro vector; es como modificar el extremo final del vector u, siempre visualmente.
  • Los escalares se representarán con una línea de trazos a modo, exclusivamente, de distinción ya que no siempre pertenecen al espacio de vectores.

Por un lado la representación del producto en el caso K = \mathbb{R} modifica, visualmente, la longitud de la imagen del vector, quedando ambos siempre superpuestos; por otro lado las representaciones en el caso K = \mathbb{C} además de modificar la longitud, también agrega rotaciones, para facilitarlas visualmente considérense centradas en el origen del vector, siendo estas modificaciones un poco más expresivas, visualmente, pero no más fáciles que en el caso real:

Vectorial space P e.GIF
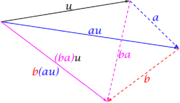
a)Decir que a(bu)=(ab)u, es exigir que los productos encadenados a(b(u)) pueden simplificarse como uno, c=ab, luego (ab)u queda como cu.
Vectorial space P a.GIF
b) Decir que existe el escalar 1 tal que 1u=u, equivale a decir exista un escalar incapaz de efectuar, mediante producto, modificación alguna a todos los vectores.
Vectorial space P b.GIF
c) Decir que a(u+v)=au+av, es exigir la propiedad distributiva respecto la suma vectorial.
Vectorial space P c.GIF
d) Decir que (a+b)u=au+bu, es exigir la propiedad distributiva respecto la suma escalar.
Vectorial space P d.GIF

Para el caso real se han de eliminar las rotaciones de los ejemplos anteriores.

Operaciones con vectores

Suma de vectores

Para sumar dos vectores libres (vector y vector) se escogen como representantes dos vectores tales que el extremo final de uno coincida con el extremo origen del otro vector.

Método del paralelogramo.
Método del triángulo.

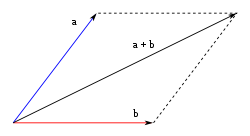
Método del paralelogramo

Este método permite solamente sumar vectores de a pares. Consiste en disponer gráficamente los dos vectores de manera que los orígenes de ambos coincidan en un punto, trazando rectas paralelas a cada uno de los vectores, en el extremo del otro y de igual longitud, formando así un paralelogramo (ver gráfico a la derecha). El resultado de la suma es la diagonal de dicho paralelogramo que parte del origen común de ambos vectores.

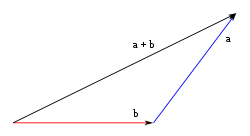
Método del triángulo

Consiste en disponer gráficamente un vector a continuación de otro; es decir, el origen de cada uno de los vectores se lleva sobre el extremo del otro. El vector resultante es aquél que nace en el origen del primer vector y termina en el extremo del último.

Método analítico para la suma y diferencia de vectores

Dados dos vectores libres,

\mathbf{a} = (a_x \mathbf{i} + a_y \mathbf{j} + a_z \mathbf{k})

\mathbf{b} = (b_x \mathbf{i} + b_y \mathbf{j} + b_z \mathbf{k})

El resultado de su suma o de su diferencia se expresa en la forma

\mathbf{a} \pm \mathbf{b} = (a_x \mathbf{i} +a_y \mathbf{j} +a_z \mathbf{k}) \pm (b_x \mathbf{i} +b_y \mathbf{j} +b_z \mathbf{k})

y ordenando las componentes,

\mathbf{a} \pm \mathbf{b} = (a_x \pm b_x) \mathbf{i} + (a_y \pm b_y) \mathbf{j} + (a_z \pm b_z)\mathbf{k}

Con la notación matricial sería

\mathbf{a} \pm \mathbf{b} = \begin{bmatrix} a_x\\ a_y\\ a_z\\\end{bmatrix} \pm \begin{bmatrix} b_x\\ b_y\\ b_z\\\end{bmatrix} = \begin{bmatrix} a_x\pm b_x\\ a_y\pm b_y\\ a_z\pm bz\\\end{bmatrix}

Conocidos los módulos de dos vectores dados, \mathbf{a} y \mathbf{b}, así como el ángulo θ que forman entre sí, el módulo de \mathbf{a} \pm \mathbf{b} es:

|\mathbf{a} \pm \mathbf{b}| = \sqrt{a^2 + b^2 - 2ab \cos \theta}

La deducción de esta expresión puede consultarse en deducción del módulo de la suma.

Producto de un vector por un escalar

Producto por un escalar.

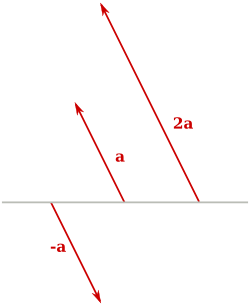
El producto de un vector por un escalar es otro vector cuyo módulo es el producto del escalar por el módulo del vector, cuya dirección es igual a la del vector, o contraria a este si el escalar es negativo.

Partiendo de la representación gráfica del vector, sobre la misma línea de su dirección tomamos tantas veces el módulo de vector como indica el escalar.

Sean p \, un escalar y \mathbf{a} un vector, el producto de p \, por \mathbf{a} se representa p \, \mathbf{a} y se realiza multiplicando cada una de las componentes del vector por el escalar; esto es,

p \, \mathbf{a} = pa_x \mathbf{i} + pa_y \mathbf{j} + pa_z \mathbf{k}

Con la notación matricial sería

p \, \mathbf{a} = p \, \begin{bmatrix} a_x\\ a_y\\ a_z\\\end{bmatrix} = \begin{bmatrix} p\,a_x\\ p\,a_y\\ p\,a_z\\\end{bmatrix}

Producto escalar

Artículo principal: Producto escalar

Producto vectorial

Artículo principal: Producto vectorial

Derivada ordinaria de un vector

Dado un vector que es función de una variable independiente

\mathbf{a}(t)= a_x(t) \mathbf{i} +a_y(t) \mathbf{j} +a_z(t) \mathbf{k}

Calculamos la derivada ordinaria del vector con respecto de la variable t, calculando la derivada de cada una de sus componentes como si de escalares se tratara:

\frac{d}{dt}\mathbf{a}(t)= \frac{d}{dt}a_x(t) \mathbf{i} + \frac{d}{dt}a_y(t) \mathbf{j} + \frac{d}{dt}a_z(t) \mathbf{k}

teniendo en cuenta que los vectores unitarios son constantes en módulo y dirección.

Con notación matricial sería

\frac{d}{dt}\mathbf{a}(t)= \frac{d}{dt} \, \begin{bmatrix} a_x\\ a_y\\ a_z\\\end{bmatrix} = \begin{bmatrix} \frac{d}{dt}a_x\\ \frac{d}{dt}a_y\\ \frac{d}{dt}a_z\\\end{bmatrix}

\mathbf{r}(t)=\sin(t) \mathbf{i}+\cos(t)\mathbf{j}+ 5t\mathbf{k}

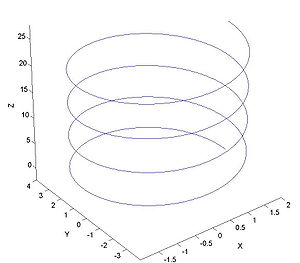
Veamos un ejemplo de derivación de un vector, partiendo de una función vectorial:

\mathbf{r}(t) = \sin(t) \mathbf{i} + \cos(t) \mathbf{j} + 5t \mathbf{k}

Esta función representa una curva helicoidal alrededor del eje z, de radio unidad, como se ilustra en la figura. Podemos imaginar que esta curva es la trayectoria de una partícula y la función \mathbf r (t)\, representa el vector posición en función del tiempo t. Derivando tendremos:

\frac{d\mathbf{r}(t)}{dt} = \frac{d}{dt}\sin(t) \mathbf{i} + \frac{d}{dt}\cos(t) \mathbf{j} + \frac{d}{dt}5t \mathbf{k}

Realizando la derivada:

\frac{d\mathbf{r}(t)}{dt} = \cos(t) \mathbf{i} - \sin (t) \mathbf{j} + 5 \mathbf{k}

La derivada del vector posición respecto al tiempo es la velocidad, así que esta segunda función determina el vector velocidad de la partícula en función del tiempo, podemos escribir:

\mathbf{v}(t) = \cos(t) \mathbf{i} - \sin(t) \mathbf{j} + 5 \mathbf{k}

Este vector velocidad es un vector tangente a la trayectoria en el punto ocupado por la partícula en cada instante. Si derivásemos de nuevo obtendríamos el vector aceleración.

Derivada covariante de un vector

Artículo principal: Derivada covariante

Cuando en lugar de emplear una "base fija" en todo el dominio de un vector se usan "bases móviles" como cuando se emplean coordenadas curvilíneas la variación total de un vector dependiente del tiempo depende no sólo de la variación de componentes como en el caso de la derivada ordinaria sino también de la variación de la orientación de la base. La variación total se llamada derivada covariante:

\frac{\delta}{\delta t}\mathbf{a}(t) = \sum_k \left(\dot{a}^k\mathbf{e}_k + a^k\dot{\mathbf{e}}_k \right) = \frac{d}{dt}\mathbf{a}(t) + \mathbf{a}(t) \times \boldsymbol{\omega}(t)

Cuando se emplea una base fija (coordenadas cartesianas) la derivada covariante coincide con la derivada ordinaria. Por ejemplo cuando se estudia el movimiento de una partícula desde un sistema de referencia no inercial en rotación, las aceleraciones de Coriolis y centrípeta se deben a los factores que contienen \boldsymbol\omega.

Ángulo entre dos vectores

El ángulo determinado por las direcciones de dos vectores \mathbf{a} y \mathbf{b} viene dado por:

\cos \theta = \frac {\mathbf a \cdot \mathbf b}{|\mathbf{a}| \, |\mathbf{b}|}

Descomposiciones de un vector

Dado un vector \mathbf{a} y una dirección de referencia dada por un vector unitario \mathbf{n} se puede descomponer el primer vector en una componente paralela y otra componente perpendicular a la dirección de referencia:

\mathbf{a} = \mathbf{a}_\| + \mathbf{a}_\bot = (\mathbf{n}\cdot\mathbf{a})\mathbf{n} + (\mathbf{n}\times \mathbf{a})\times \mathbf{n}

En física esta descomposición se usa en diferentes contextos como descomponer la aceleración en una componente paralela a la velocidad y otra componente perpendicular a la misma. También el tensión mecánica en un punto sobre un plano puede descomponerse en una componente normal al plano y otra paralela.

También dado un campo vectorial \mathbf{u}(\mathbf{x}) definido sobre un dominio de Lipschitz, acotado, simplemente conexo y de cuadrado integrable \mathbf{u}\in (L^2(\Omega))^3 admite la llamada descomposición de Helmholtz como suma de un campo conservativo y un campo solenoidal:

\mathbf{u} = \mathbf{u}_C + \mathbf{u}_S = (\boldsymbol{\nabla}\varphi) + (\boldsymbol{\nabla}\times \mathbf{A})

Cambio de base vectorial

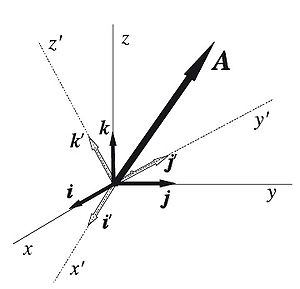
Cambio de base vectorial.

En matemáticas las rotaciones son transformaciones lineales que conservan las normas en espacios vectoriales en los que se ha definido una operación de producto interior. La matriz de transformación tiene la propiedad de ser una matriz unitaria, es decir, es ortogonal y su determinante es 1. Sea un vector \scriptstyle \mathbf A expresado en una sistema de coordenadas cartesianas (x, y, z) con una base vectorial \mathcal{B} asociada definida por los versores \left( \mathbf i, \mathbf j,\mathbf k\, \right); esto es,

\mathbf A=\begin{bmatrix} A_x \\ A_y \\ A_z \end{bmatrix}_{\mathcal{B}}

Ahora, supongamos que giramos el sistema de ejes coordenados, manteniendo fijo el origen del mismo, de modo que obtengamos un nuevo triedro ortogonal de ejes (x′, y′, z′), con una base vectorial \mathcal{B}' asociada definida por los versores \left( \mathbf i', \mathbf j',\mathbf k'\, \right). Las componentes del vector \mathbf A \, en esta nueva base vectorial serán:

\mathbf A=\begin{bmatrix} A'_x \\ A'_y \\ A'_z \end{bmatrix}_{\mathcal{B}'}

La operación de rotación de la base vectorial siempre puede expresarse como la acción de un operador lineal (representado por una matriz) actuando sobre el vector (multiplicando al vector):

\mathbb R \, \mathbf A_{\mathcal{B}} = \mathbf A_{\mathcal{B}'}

que es la matriz de transformación para el cambio de base vectorial.

Cambio de base vectorial.
Ejemplo

En el caso simple en el que el giro tenga magnitud \theta\, alrededor del eje z, tendremos la transformación:

\mathbb R = \begin{bmatrix} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta& 0 \\ 0 & 0 & 1 \\ \end{bmatrix}

Al hacer la aplicación del operador, es decir, al multiplicar la matriz por el vector, obtendremos la expresión del vector \mathbf A \, en la nueva base vectorial:

\begin{bmatrix} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta& 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} A_x \\ A_y \\ A_z \end{bmatrix}_{\mathcal{B}} = \begin{bmatrix} A'_x \\ A'_y \\ A'_z \end{bmatrix}_{\mathcal{B}'}

siendo

A'_x = A_x \cos\theta + A_y\sin\theta\,
A'_y = -A_x \sin\theta + A_y\cos\theta\,
A'_z = A_z \,

las componentes del vector en la nueva base vectorial.

Requerimientos físicos de las magnitudes vectoriales

No cualquier n-tupla de funciones o números reales constituye un vector físico. Para que una n-tupla represente un vector físico, los valores numéricos de las componentes del mismo medidos por diferentes observadores deben transformarse de acuerdo con ciertas relaciones fijas.

En mecánica newtoniana generalmente se utilizan vectores genuinos, llamados a veces vectores polares, junto con pseudovectores, llamados vectores axiales que realmente representan el dual de Hodge de magnitudes tensoriales antisimétricas. El momento angular, el campo magnético y todas las magnitudes que en cuya definición interviene el producto vectorial son en realidad pseudovectores o vectores axiales.

En teoría especial de la relatividad, sólo los vectores tetradimensionales cuyas medidas tomadas por diferentes observadores pueden ser relacionadas mediante alguna transformación de Lorentz constituyen magnitudes vectoriales. Así las componentes de dos magnitudes vectoriales medidas por dos observadores O\, y \bar{O} deben relacionarse de acuerdo con la siguiente relación:

\bar{V}^\beta = \sum_{\alpha=0}^3 \Lambda_\alpha^\beta \ V^\alpha


Donde \Lambda_\alpha^\beta son las componentes de la matriz que da la transformación de Lorentz. Magnitudes como el momento angular, el campo eléctrico o el campo magnético o el de hecho en teoría de la relatividad no son magnitudes vectoriales sino tensoriales.

Véase también

Referencias

  1. ↑ a b c Ito, Kiyosi (1993), Encyclopedic Dictionary of Mathematics (2da edición), MIT Press, ISBN 978-0-262-59020-4 
  2. ↑ a b c «Vectors and Direction» (en inglés). The Physics Classroom. Consultado el 3 de junio de 2010.
  3. ↑ a b c «Vector» (en inglés). mathwords.com. Consultado el 3 de junio de 2010.
  4. ↑ A.B. Ivanov. Michiel Hazewinkel (ed.): «Vector» (en inglés). Encyclopaedia of Mathematics. Springer. Consultado el 13 de junio de 2010.
  5. ↑ «Euclidean vector» (en inglés). PlanetMath.org. Consultado el 3 de junio de 2010.
  6. ↑ «Vector» (en inglés). Math Academy Online. Consultado el 3 de junio de 2010.

Bibliografía

  • Ortega, Manuel R. (1989-2006) (en español). Lecciones de Física (4 volúmenes). Monytex. ISBN 84-404-4290-4, ISBN 84-398-9218-7, ISBN 84-398-9219-5, ISBN 84-604-4445-7. 
  • Resnick,Robert & Krane, Kenneth S. (2001) (en inglés). Physics. New York: John Wiley & Sons. ISBN 0-471-32057-9. 
  • Serway, Raymond A.; Jewett, John W. (2004) (en inglés). Physics for Scientists and Engineers (6ª edición). Brooks/Cole. ISBN 0-534-40842-7. 
  • Tipler, Paul A. (2000) (en español). Física para la ciencia y la tecnología (2 volúmenes). Barcelona: Ed. Reverté. ISBN 84-291-4382-3. 

Enlaces externos


Wikimedia foundation. 2010.

Игры ⚽ Нужен реферат?
Sinónimos:
, , ,


Mira otros diccionarios:

  • Vector — may refer to: In mathematics * Euclidean vector, a geometric entity endowed with both length and direction, an element of a Euclidean vector space * Coordinate vector, in linear algebra, an explicit representation of an element of any abstract… …   Wikipedia

  • vector — VECTÓR, vectori, s.m. Mărime matematică sau fizică definită printr o valoare numerică, o unitate de măsură, o direcţie şi un punct de aplicaţie (reprezentată grafic printr un segment de dreaptă orientat). ♢ (Adjectival) Rază vectoare. – Din fr.… …   Dicționar Român

  • Vector WX-8 — Vector WX 8 …   Википедия

  • vector — m. microb. Hospedador intermediario que transporta y transmite un microorganismo patógeno productor de enfermedad. Pueden ser mamíferos, artrópodos, etc. También se denomina vehículo. ⊆ genét. Plásmido o cromosoma vírico en cuyo genoma se inserta …   Diccionario médico

  • Vector — Vec tor, n. [L., a bearer, carrier. fr. vehere, vectum, to carry.] 1. Same as {Radius vector}. [1913 Webster] 2. (Math.) A directed quantity, as a straight line, a force, or a velocity. Vectors are said to be equal when their directions are the… …   The Collaborative International Dictionary of English

  • Vector — steht für in der Informatik ein eindimensionales Array einen Vektorprozessor den Sportwagenhersteller Vector Motors Corporation sowie dessen Fahrzeugmodelle. die Linuxdistribution VectorLinux die Vector Informatik, eine auf Software Tools und… …   Deutsch Wikipedia

  • VECTOR — apud Treb. Pollionem, in Gallienis, c. 12. Quum taurum ingentem in arenam misisset, exîssetque ad eum feriendum vector, neque perductum decies potuisset occidere etc. venator est, sic dictus ex Graeco δ᾿έκτης, quod opuds sit viribus maximis ad… …   Hofmann J. Lexicon universale

  • vector — (Del lat. vector, ōris, que conduce). 1. m. Agente que transporta algo de un lugar a otro. U. t. c. adj.) 2. Bioquím. Fragmento de ácido desoxirribonucleico que puede unir otro fragmento ajeno y transferirlo al genoma de otros organismos. 3. Fil …   Diccionario de la lengua española

  • Vector — (Math.), s. Radius vector …   Pierer's Universal-Lexikon

  • Vector — (Radius vector), »Fahrstrahl«, Leitstrahl; s. Radius und Kegelschnitte; vgl. Vektoranalysis …   Meyers Großes Konversations-Lexikon

  • vector — (n.) quantity having magnitude and direction, 1704, from L. vector one who carries or conveys, carrier, from pp. stem of vehere carry, convey (see VEHICLE (Cf. vehicle)) …   Etymology dictionary

Compartir el artículo y extractos

Link directo
… Do a right-click on the link above
and select “Copy Link”