- Circuito RLC
-
En electrodinámica, un circuito RLC es un circuito lineal que contiene una resistencia eléctrica, una bobina (inductancia) y un condensador (capacidad).
Existen dos tipos de circuitos RLC, en serie o en paralelo, según la interconexión de los tres tipos de componentes. El comportamiento de un circuito RLC se describen generalmente por una ecuación diferencial de segundo orden (en donde los circuitos RC o RL se comportan como circuitos de primero orden).
Con ayuda de un generador de señal, es posible inyectar en el circuito oscilaciones y observar en algunos casos el fenómeno de resonancia, caracterizado por un aumento del corriente (ya que la señal de entrada elegida corresponde a la pulsación propia del circuito, calculable a partir de la ecuación diferencia que lo rige).
Contenido
Circuito RLC en serie
 Circuito RLC en serie.
Circuito RLC en serie.
Circuito sometido a un escalón de tensión
Si un circuito RLC en serie es sometido a un escalón de tensión
 , la ley de las mallas impone la relación:
, la ley de las mallas impone la relación:Introduciendo la relación característica de un condensador:
Se obtiene la ecuación diferencial de segundo orden:
Donde:
- E es la fuerza electromotriz de un generador, en voltios (V);
- uC es la tensión en los bornes de un condensador, en voltios (V);
- L es la inductancia de la bobina, en henrys (H);
- i es la intensidad de corriente eléctrica en el circuito, en amperios (A);
- q es la carga eléctrica del condensador, en coulombs (C);
- C es la capacidad eléctrica del condensador, en farads (F);
- Rt es la resistencia total del circuito, en ohmios (Ω);
- t es el tiempo en segundos (s)
En el casos de un régimen sin pérdidas, esto es para
 , se obtiene una solución de la forma:
, se obtiene una solución de la forma:Donde:
- T0 el periodo de oscilación, en segundos;
- φ la fase en el origen (lo más habitual es elegirla para que φ = 0)
Lo que resulta:
Donde f0 es la frecuencia de resonancia, en hertz (Hz).
Circuitos sometidos a una tensión sinusoidal
La transformación compleja aplicada a las diferentes tensiones permite escribir la ley de las mallas bajo la forma siguiente:
siendo, introduciendo las impedancias complejas:
La frecuencia angular de resonancia en intensidad de este circuito ω0 es dada por:
Para esta frecuencia la relación de arriba se convierte en:

- y se obtiene:

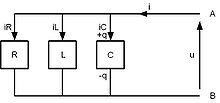
Circuitos RLC en paralelo



ya que



Atención, la rama C es un corto-circuito: no se pueden unir las ramas A y B directamente a los bornes de un generador E, se les debe adjuntar una resistencia.
Las dos condiciones iniciales son:
- il0 conserva su valor antes de la puesta en tensión (porque la inductancia se opone a la variación de corriente).
- q0 conserva su valor antes de la puesta en tensión
 .
.
Circuito sometido a una tensión sinusoidal
La transformación compleja aplicada a las diferentes intensidades proporciona:
Siendo, introduciendo las impedancias complejas:

- siendo :
![\underline I = \left[ \frac{1}{R} + j (C \omega - \frac{1}{L \omega}) \right] \underline U](4/8640a8358611b48e02390533687a5b8d.png)
La frecuencia angular de resonancia en intensidad de este circuito ω0 es dada por:
Para esta frecuencia la relación de arriba se convierte en:

- y se obtiene:

Utilización de los circuitos RLC
Los circuitos RLC son generalmente utilizados para realizar filtros de frecuencias, o de transformadores de impedancia. Estos circuitos pueden entonces comportar múltiples inductancias y condensadores: se habla entonces de "red LC".
Un circuito LC simple es denominado de segundo orden porque su función de transferencia comporta un polinomio de segundo grado en el denominador.
Véase también
- Circuito RC
- Circuito RL
- Circuito LC
Enlaces externos
Categorías:- Sistemas oscilantes
- Circuitos electrónicos
Wikimedia foundation. 2010.








![\underline {U_G} = - \frac{j}{C \omega} \underline I + j L \omega \underline I + R_{t} \underline I = \bigg[ R_t + j \frac{LC \omega^2 - 1}{C \omega} \bigg] \underline I](2/a3299971c511a4b8b5c8957f837aca51.png)