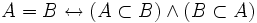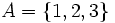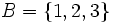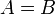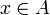El axioma de extensionalidad establece algo en apariencia tan trivial como que dos conjuntos son iguales si y sólo si tienen los mismos elementos. La forma de saber si tienen los mismos elementos no es otra que mirar uno a uno los elementos de cada conjunto y ver si pertenecen también al otro. Es decir:

Ejemplo 1

Si tenemos los conjuntos:

El axioma de extensionalidad nos dice que los conjuntos A y B son iguales.

Los conjuntos matemáticos no tienen identidad por sí mismos. Su identidad depende únicamente de los elementos que lo integran. Si quitamos de A el elemento 3, el resultado no es A con un elemento menos sino otro conjunto que es distinto de A. Los conjuntos matemáticos no se comportan en ese sentido como cajas donde se pueden guardar cosas.

El axioma de extensionalidad establece en qué sentido se puede usar la relación:

Ejemplo 2

Alguien puede afirmar: éste es mi coche, ésta es mi casa y éste es mi perro indicando con ello una cierta relación de pertenencia. Esa relación de pertenencia, sin embargo, no es matemática ya que implicaría que esa persona es un conjunto y que su identidad le viene dada por lo que le pertenece. Llegado el caso de que cambiara de coche, de casa o de perro, necesariamente tendría que ser otra persona, lo que no es el caso.

Hay casos más difíciles que el anterior, donde los objetos que se estudian parecen verdaderos conjuntos matemáticos. Un caso muy cercano es el de las categorías de Wikipedia. Nada más natural que considerarlas como conjuntos matemáticos cuyos elementos son los artículos que contienen. Esto sin embargo no es verdad como puede verse por el siguiente ejemplo.

Ejemplo 3

Imaginemos (mentalmente para evitar WP:NSW) que creamos el Artículo 1, el Artículo 2 y el Artículo 3 y los categorizamos en la Categoría A y la Categoría B. Es fácil comprobar que a pesar de que ambas categorías tienen los mismos elementos no se sigue de ello que:

Categoría A = Categoría B.

Las categorías de Wikipedia no son por tanto verdaderos conjuntos matemáticos.

Estos ejemplos sirven para mostrar que el establecimiento de este axioma en la teoría de conjuntos no es un asunto trivial. En realidad este axioma define qué conjuntos son matemáticamente válidos para luego poder manipularlos con el resto de los axiomas.

Véase también

• Axiomas de Zermelo-Fraenkel