- Teorema de Ceva
-
El teorema de Ceva, caso 1: las tres líneas son concurrentes en un punto O dentro de ABC.
El teorema de Ceva, caso 2: el punto O se encuentra fuera de ABC.El teorema de Ceva es un teorema de geometría elemental.
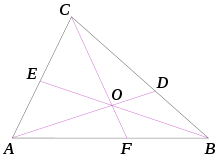
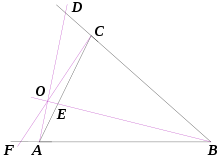
El teorema establece que dado un triángulo ABC, y los puntos D, E, y F que se encuentran sobre los lados BC, CA, y AB respectivamente, los segmentos AD, BE y CF son concurrentes si y solo si
donde AF es la distancia entre A y F (la distancia en una dirección sobre una línea es definida como positiva, y en la dirección opuesta es definida como de signo negativo).
Existe una forma trigonométrica equivalente del teorema de Ceva, que establece que , AD,BE,CF son concurrentes si y solo si
El teorema fue demostrado en 1678 por Giovanni Ceva en su trabajo De lineis rectis, pero con anterioridad por Yusuf Al-Mu'taman ibn Hűd, un rey de la taifa de Zaragoza del siglo XI.
Véase también
- Teorema de Menelaus - el dual del teorema de Ceva
- Geometría proyectiva
- Mediana (geometría) - un caso de su uso
Referencias
- Grünbaum, Branko; Shephard, G. C. (1995), «Ceva, Menelaus and the Area Principle», Mathematics Magazine 68 (4): 254–268, doi:, http://links.jstor.org/sici?sici=0025-570X(199510)68%3A4%3C254%3ACMATAP%3E2.0.CO%3B2-0.
- J. B. Hogendijk, "Al-Mutaman ibn Hűd, 11the century king of Saragossa and brilliant mathematician," Historia Mathematica 22 (1995) 1-18.
- Landy, Steven. A Generalization of Ceva's Theorem to Higher Dimensions. The American Mathematical Monthly, Vol. 95, No. 10 (Dec., 1988), pp. 936-939
- Masal'tsev, L. A. (1994) "Incidence theorems in spaces of constant curvature." Journal of Mathematical Sciences, Vol. 72, No. 4
- Wernicke, Paul. The Theorems of Ceva and Menelaus and Their Extension. The American Mathematical Monthly, Vol. 34, No. 9 (Nov., 1927), pp. 468-472
Enlaces externos
- Menelaus y Ceva en MathPages
- Bogomolny, Alexander. «Ceva's Theorem» (en inglés). Interactive Mathematics Miscellany and Puzzles.
- Bogomolny, Alexander. «Trigonometric Form of Ceva's Theorem» (en inglés). Interactive Mathematics Miscellany and Puzzles.
- Glossary of Encyclopedia of Triangle Centers includes definitions of cevian triangle, cevian nest, anticevian triangle, Ceva conjugate, and cevapoint
- Conics Associated with a Cevian Nest, by Clark Kimberling
- Warendorff, Jay. «Ceva's Theorem» (en inglés). The Wolfram Demonstrations Project. Wolfram Research.
- Weisstein, Eric W. «Ceva's Theorem» (en inglés). MathWorld. Wolfram Research.
Categorías:- Geometría del triángulo
- Teoremas de geometría
Wikimedia foundation. 2010.
