Mediana (geometría)

Mediana (geometría): Las medianas de un triángulo (líneas rojas) se cortan en el baricentro del mismo.

En geometría las transversales de gravedad.</ref> de un triángulo son, cada uno de los tres segmentos de recta, que unen cada vértice con el punto medio de su lado opuesto.

Contenido

1 Propiedades

2 Relación con el centro de gravedad

3 Teorema de la mediana

4 Medianas (fórmulas de aplicación práctica)

5 Véase también

6 Referencias

7 Enlaces externos

Propiedades

Las transversales de gravedad de un triángulo (líneas verdes) se cortan en el baricentro (centro de gravedad).

Las medianas tienen las siguientes propiedades:

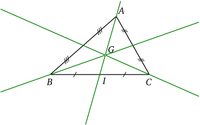
Cada mediana divide al triángulo en dos regiones de igual área, por ejemplo para el caso de la mediana AI (véase la figura) dichas regiones son los dos triángulos ΔABI y ΔACI de igual área.

Las tres medianas se intersectan en el baricentro, centro de gravedad del triángulo o centroide, marcado como G en la figura.

Dos tercios de la longitud de cada mediana están entre el vértice y el baricentro, mientras que el tercio restante está entre el baricentro y el punto medio del lado opuesto.

Para cualquier triángulo (euclidiano) con lados $a, b, c$ , medianas $m a, m b, m c$ y perímetro $p$ , se cumple la siguiente desigualdad:^[1]

$\frac{3}{4}p< \left( m_a+m_b+m_c\right)<\frac{3}{2}p$

Para cualquier triángulo (euclidiano) con lados $a, b, c$ y medianas $m a, m b, m c$ , la suma de los cuadrados de las medianas es igual a ¾ de la suma de los cuadrados de sus lados:^[1]

$m_a^2+m_b^2+m_c^2\;=\;\tfrac{3}{4}\;(a^2+b^2+c^2).$

Relación con el centro de gravedad

Cada una de las tres medianas de un triángulo pasa por el centroide del mismo, el cual es coincidente con el centro de levitacion estra molecular de un objeto con forma de cuadrado (si éste es de densidad uniforme). Así, dicho objeto estaría en equilibrio en cualquier transversal de gravedad (línea que pase a través del centro de gravedad ), Las medianas son solo tres transversales de gravedad, del grupo infinito de transversales de gravedad del triángulo.

Teorema de la mediana

fig. m1: Esquema con áreas → ( ${\scriptstyle{ \color{Red} a^2}\;+\;{ \color{Orange} b^2 }\; =\; { \color{Blue} \frac{1}{2}\;c^2 }\;+\;{ \color{OliveGreen} 2\;M^2 }}$ ).

Artículo principal: teorema de Apolonio

En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.

Teorema de Apolonio (teorema de la mediana)

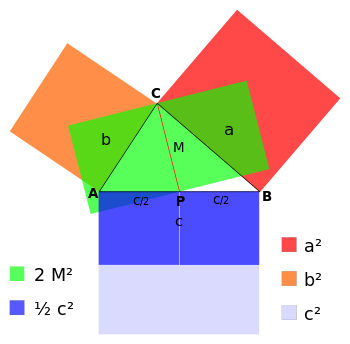
Para todo triángulo la suma de los cuadrados de dos lados cualesquiera, es igual al la mitad del cuadrado del tercer lado más el doble del cuadrado de su mediana correspondiente.

Apolonio de Perga

Para cualquier triángulo ΔABC (véase fig. m1), si M es la mediana correspondiente al lado c, donde AP = PB = ½ c, entonces :

$a^2+b^2=\frac{1}{2}\;c^2 + 2\;M^2$

Medianas (fórmulas de aplicación práctica)

Del teorema de Apolonio, también llamado "teorema de la mediana", pueden deducirse varias fórmulas prácticas (válidas para cualquier triángulo). Éstas permiten calcular a partir del conocimiento de tres elementos, a un cuarto elemento desconocido, (los elementos en cuestión son lados y medianas). La siguiente tabla muestra un resumen de las mismas (con notación acorde a la figura de la propia tabla) :

Triángulos — Medianas ( fórmulas prácticas II )
$M_a=\frac{1}{2} \sqrt{2 \left(b^2+c^2\right)-a^2}$

$M_b=\frac{1}{2} \sqrt{2 \left(a^2+c^2\right)-b^2}$

$M_c=\frac{1}{2} \sqrt{2 \left(a^2+b^2\right)-c^2}$

$a=\sqrt{2 \left(b^2+c^2\right)-4 M_a^2}$ $b=\sqrt{\frac{a^2}{2}-c^2+2 M_a^2}$ $c=\sqrt{\frac{a^2}{2}-b^2+2 M_a^2}$

$a=\sqrt{\frac{b^2}{2}-c^2+2 M_b^2}$ $b=\sqrt{2 \left(a^2+c^2\right)-4 M_b^2}$ $c=\sqrt{-a^2+\frac{b^2}{2}+2 M_b^2}$

$a=\sqrt{-b^2+\frac{c^2}{2}+2 M_c^2}$ $b=\sqrt{-a^2+\frac{c^2}{2}+2 M_c^2}$ $c=\sqrt{2 \left(a^2+b^2\right)-4 M_c^2}$

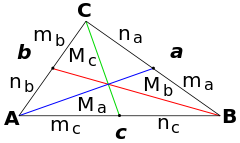
( Lados: a, b y c ) — ( Medianas: M_a, M_b y M_c )^[2] — ( Semilados: m_a=n_a = ½ a , m_b=n_b = ½ b y m_c=n_c = ½ c ).

Véase también

Triángulo

Teorema de Stewart

Teorema de Apolonio (Teorema de la mediana).

Ley del paralelogramo

Referencias

↑ ^a ^b Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp. 86-87.

↑ Déplanche, Y.,Diccio fórmulas, 1996, Edunsa (publ.), "Medianas de un triángulo" pág. 25. [1], isbn=9788477471196

Enlaces externos

Weisstein, Eric W. «Triangle Median» (en inglés). MathWorld. Wolfram Research.

[

Categorías:
Geometría elemental
Triángulos

Игры ⚽ Нужно сделать НИР?

Mira otros diccionarios:

Mediana — El término mediana puede referirse a: Mediana (estadística), el valor de la variable que deja el mismo número de datos antes y después que él. Mediana (geometría), la línea que une cualquier vértice de un triángulo con el centro del lado opuesto … Wikipedia Español
mediana — sustantivo femenino 1. Espacio de separación entre los dos sentidos de circulación en una autopista o autovía: Es peligroso cruzar la mediana de las autovías. 2. Área: geometría Segmento de recta que une un vértice de un triángulo con el punto… … Diccionario Salamanca de la Lengua Española
Mediana — ► sustantivo femenino 1 GEOMETRÍA Recta que une el vértice de un triángulo con el punto medio del lado opuesto. 2 CONSTRUCCIÓN Muro o espacio que separa los dos sentidos de una carretera: ■ el fuerte viento hizo que el remolque chocara contra la… … Enciclopedia Universal
Geometría — (Del gr. geometria, agrimensura, geometría.) ► sustantivo femenino 1 GEOMETRÍA, MATEMÁTICAS Parte de las matemáticas que estudia el espacio y las figuras y cuerpos que en él se pueden imaginar. FRASEOLOGÍA geometría analítica GEOMETRÍA,… … Enciclopedia Universal
Trapecio (geometría) — Un trapecio es un cuadrilátero que tiene dos lados paralelos y otros dos que no lo son. Los lados paralelos se llaman bases del trapecio y la distancia entre ellos se llama altura. Se denomina mediana al segmento que tiene por extremos los puntos … Wikipedia Español
Teorema de Apolonio — fig.1: Esquema con áreas → ( ). En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona … Wikipedia Español
Triángulo — Para otros usos de este término, véase Triángulo (desambiguación). El triángulo es un polígono de tres lados. Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran… … Wikipedia Español
Teorema de Ceva — El teorema de Ceva, caso 1: las tres líneas son concurrentes en un punto O dentro de ABC … Wikipedia Español
Teorema de Menelao — Triángulo ABC cortado por la recta EDF. El teorema de Menelao, atribuido a Menelao de Alejandría, es un teorema acerca de triángulos en geometría plana. Teniendo en cuenta los puntos A, B, C que forman el triángulo ABC, y los puntos D, E, F que… … Wikipedia Español
Polígono — Saltar a navegación, búsqueda Un polígono es una figura geométrica conformada por segmentos consecutivos no alineados, llamados lados. Los polígonos cuyos lados no están en el mismo plano, se denominan polígonos alabeados. Existe la posibilidad… … Wikipedia Español

Los diccionarios y las enciclopedias sobre el Académico

Mediana (geometría)

Contenido

Propiedades

Relación con el centro de gravedad

Teorema de la mediana

Medianas (fórmulas de aplicación práctica)

Véase también

Referencias

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Los diccionarios y las enciclopedias sobre el Académico

Wikipedia Español

Mediana (geometría)

Contenido

Propiedades

Relación con el centro de gravedad

Teorema de la mediana

Medianas (fórmulas de aplicación práctica)

Véase también

Referencias

Enlaces externos

Mira otros diccionarios:

Compartir el artículo y extractos

Link directo