Teorema de Viviani

La suma de las longitudes, ℓ + m + n, es igual a la altura del triángulo.

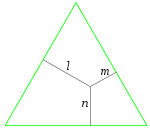
El teorema de Viviani, llamado así en honor de Vincenzo Viviani, enuncia que la suma de las distancias desde un punto a cada uno de los lados de un triángulo equilátero es igual a la la altura del triángulo.

El teorema se puede extender a polígonos equiláteros y polígonos equiangulares. Específicamente, la suma de las distancias desde un punto hasta los lados de un polígono equilátero o equiangular no depende del punto.^[1]

Demostración

Este teorema se puede demostrar fácilmente comparando áreas de triángulos. Sea ABC un triángulo equilátero donde h es la altura y s la longitud de cada lado. P es un punto arbitrario en el interior del triángulo, y ℓ, m, n son las distancias entre P y cada uno de los lados. Entonces el área de ABC es

que es lo que se buscaba.

Aplicaciones

Diagrama de inflamabilidad del metano.

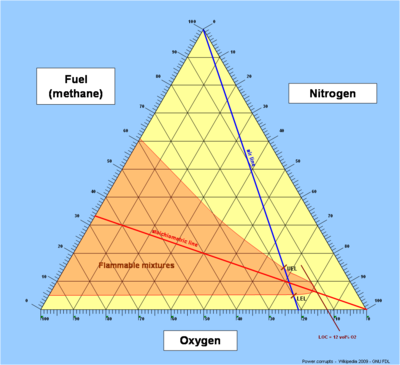
Gracias al teorema de Viviani, se pueden utilizar rectas paralelas a los lados de un triángulo equilátero para dar coordenadas para diagramas ternarios tales como los diagramas de inflamabilidad. De forma más general, se pueden utilizar coordenadas en un simplex regular de la misma manera.

Referencias

• 1. ↑ Elias Abboud "On Viviani’s Theorem and its Extensions" pp. 2, 11 (en inglés)
• Weisstein, Eric W. «Viviani's Theorem» (en inglés). MathWorld. Wolfram Research.

Enlaces externos

• Viviani's Theorem: What is it? en Cut the knot, en inglés.
• Viviani's Theorem por Jay Warendorff (Wolfram Demonstrations Project), en inglés.