- Profundidad de color
-
Profundidad de color
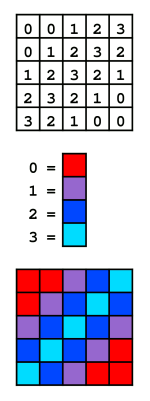 Paleta de colores.
Paleta de colores.
La profundidad de color o bits por pixel es un concepto de la computación gráfica que se refiere a la cantidad de bits de información necesarios para representar el color de un píxel en una imagen digital o en un framebuffer. Debido a la naturaleza del sistema binario de numeración, una profundidad de bits de n implica que cada píxel de la imagen puede tener 2n posibles valores y por lo tanto, representar 2n colores distintos.
Debido a la aceptación prácticamente universal de los octetos de 8 bits como unidades básicas de información en los dispositivos de almacenamiento, los valores de profundidad de color suelen ser divisores o múltiplos de 8, a saber 1,2,4,8,16,24 y 32, con la excepción de la profundidad de color de 15, usada por ciertos dispositivos gráficos.
Contenido
Color indexado
Para las profundidades de color inferiores o iguales a 8, los valores de los pixeles hacen referencia a tonos RGB indexados en una tabla, llamada habitualmente mapa de colores o paleta. Los tonos en dicha tabla pueden ser definidos por convención o bien ser configurables, en función de la aplicación que la defina. A continuación se mencionarán algunas profundidades de color en la gama baja, así como la cantidad de tonos que pueden representar en cada pixel y el nombre que se le otorga a las imágenes o framebuffers que los soportan.
- 1 bit por píxel: 21 = 2 colores, también llamado monocromo.
- 2 bits por píxel: 22 = 4 colores, o CGA.
- 4 bits por píxel: 24 = 16 colores, la cual es la mínima profundidad aceptada por el estándar VGA.
- 8 bits por píxel: 28 = 256 colores, también llamado Super VGA.
Color directo
Cuando los valores de la profundidad de colores aumentan, se torna impráctico mantener una tabla o mapa de colores debido a la progresión exponencial de la cantidad de valores que el pixel puede tomar. En esos casos se prefiere codificar dentro de cada pixel los tres valores de intensidad luminosa que definen un color cualquiera en el modelo de color RGB.
Color de alta resolución o HiColor
Los valores de profundidad de color de 15 y 16 bits son llamados habitualmente color de alta resolución o HiColor.
- En la profundidad de 15 bpp se utilizan 5 bits para codificar la intensidad del rojo, 5 para el verde y los otros 5 para el azul. Con una profundidad de 15 bpp es posible representar 32x32x32 = 32768 colores en cada pixel.
- En la profundidad de 16 bpp se utilizan 5 bits para codificar la intensidad del rojo, 6 para el verde y los otros 5 para el azul. La razón de esto es que experimentalmente se sabe que el ojo humano es más sensible al color verde, y que puede discriminar más tonos que varían ligeramente en la intensidad verde. Con la profundidad de 16 bpp es posible representar 32x64x32 = 65536 colores en cada pixel. El tamaño de la imagen dependerá de la profundidad de bit.
Color real o True Color
Para la profundidad de color de 24 bits por pixel, se habla de color verdadero debido a que la policromía se acerca a lo que el ojo humano puede encontrar en el mundo real, y a que dicho ojo humano se torna incapaz de diferenciar entre un tono y otro, si la diferencia se mantiene en un cierto rango mínimo. En la profundidad de color de 24 bits por pixel, se dedica un octeto entero a representar la intensidad luminosa de cada uno de los tres tonos primarios de rojo, verde y azul, lo cual permite que cada pixel pueda tomar 224 = 256x256x256 = 16.777.216 colores distintos.
Cuando se utilizan 32 bits para representar un color se agrega al esquema de 256 valores para cada tono primario un cuarto canal denominado alfa que representa la transparencia. Este valor se utiliza cuando se deben superponer dos imágenes.
Edwin Catmull propuso una serie de operadores para la mezcla (también llamado blend) de imágenes. Debido a que Catmull estaba desarrollando el sistema de animación de Pixar necesitaba automatizar la composición de imágenes. Juntamente con Marc Levoy (Levoy los desarrollo por su cuenta en los estudios Hanna Barbera) sentaron las bases del álgebra de colores. El operador más común es el OVER, que presentamos a continuación:
Dados los colores A [r1, g1, b1, a1] y B [r2, g2, b2, a2], el resultado de mezclar: A sobre B es:
A OVER B = [ r1 * a1 + r2(1 - a1), g1 * a1 + g2(1 - a1), b1 * a1 + b2(1 - a1) ]
Notemos que el orden es importante: A over B es diferente que B over A. Esta es la razón por la cual la transparencia se debe aplicar en orden. Por ejemplo si tenemos tres imágenes A, B y C, donde C es el fondo y A es la imagen al frente, el orden es el siguiente: Imagen Final = A over ( B over C ) Existen otros operadores importantes como el OUT, ADD, SUB y otras formulaciones de OVER más complejas.
Véase también
Enlaces externos
Categorías: Infografía | Color | Computación gráfica
Wikimedia foundation. 2010.
